السلام عليكم ورحمة الله تعالى وبركاته، هذا الدرس الأول من الفصل الثاني من كتاب «استيعاب الخوارزميات Grokking Algorithms»، الذي سبق وشرحنا الفصل الأول، تجده هنا!
متطلبات هذا الدرس أن تدرس الفصل الأول وتفهمه فهمًا، فهو الأساس الذي سنبني عليه بقية فصول الكتاب، فكل فصلٍ مبني على الفصل الذي سبقه.
الدرس الأول: هنا.
الدرس الثاني: هنا.
الدرس الأخير: هنا.
عمل الذاكرة
افترض أن لديك خزانة بها أدراج، كل درج يتسع لشيء واحد فقط، لا يمكن تخزين شيئين في درج واحد، وعندك مظلة ودمية، وعندك خادم اسمه عبود، فتطلب منه درجين لتخزين المظلة والدمية.

فيفتحمها ويضع الدمية في درج والمظلة في درج آخر.

أتعلم؟ لقد تعلمت الآن كيفية عمل ذاكرة الحاسوب!
فذاكرة الحاسوب ليست إلا خزانة كبيرة بها أدراج كثيرة، كل درج له عنوان، لكي تعلم في أي درج وضعت غرضك، لأن الخزانة ضخمة وعدد الأدراج يصل للآلاف!
هذه الصورة بها عنوان الدرج:
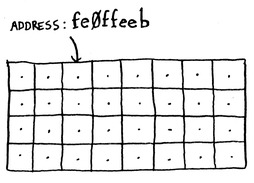
هذا fe0ffeeb هو العنوان، مكتوب بنظام العد السِّتَ عَشرِيّ hexadecimal، لخانة في الذاكرة. فما الذاكرة إلا مجموعة خانات نخزن فيها قيم فقط.
في كل مرة تطلب من الحاسوب تخزين عنصر أو قيمة في الذاكرة، بإنشاء متغير، فأنت تسأله إن كان عنده مساحة، فإن كانت عنده أعطاك عنوان تلك الخانة في الذاكرة لتخزين القيمة.
ماذا لو أردت تخزين مجموعة عناصر أو قيم متعددة؟
عندنا طريقتان: اللائحة المرتبطة linked list والصفيفة array، أشهر بنيتا معطيات مستخدمة في بنى المعطيات data structures، وهما موضوعا مقالنا لليوم، سأذكر محاسن ومساوئ كل واحدة بمقارنة بينهما. ووجب التنبيه أن لا طريقة أفضل من أخرى، فهذا يعتمد على غرضك، فلكل غرض طريقة.
افترض أنك تكتب بُريمجًا لإدارة المهام todos، وستخزن المهام المناطة بك في الذاكرة في لائحة. هل تستخدم الصفيفة أم اللائحة المترابطة؟
سأبدأ أولًا بالصفيفة ثم اللائحة المترابطة.
الصفيفة array
لديك ثلاث مهام شراء الشاي والغداء من الخارج وأيضًا شراء بوشي bocce، سنخزن المهام في صفيفة، وباستعمال الصفيفة فإن المهام ستكون مخزنة في خانات متجاورة في الذاكرة، الخانة الأولى بجوار الثانية، والثانية بجوار الثالثة وهكذا دواليك…
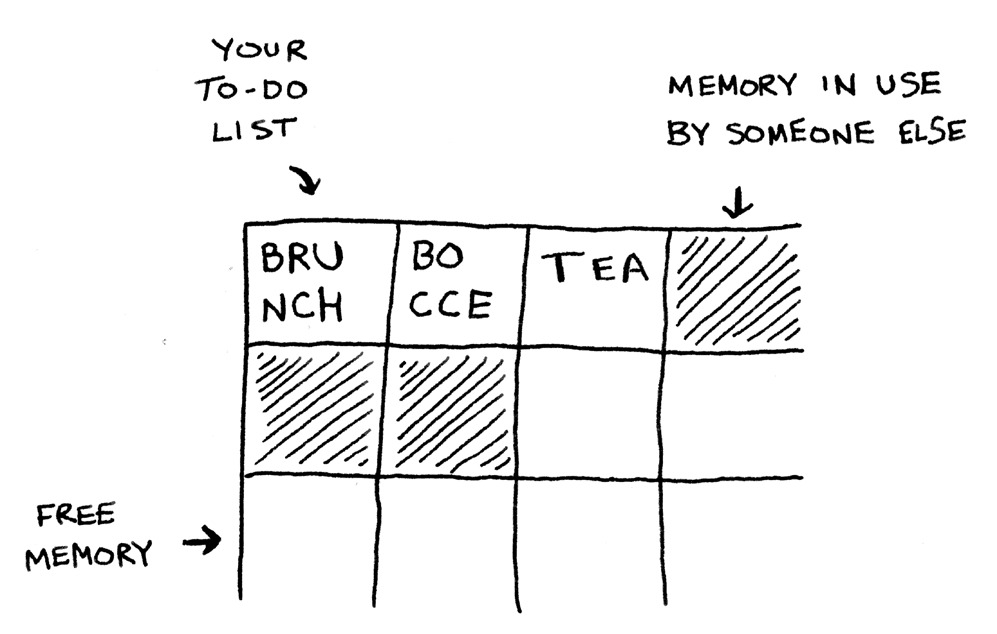
المهام مكتوبة في الخانات الثلاث على اليسار، أما الخانة المحتوية على الخطوط فإنه مستعملة، أحدهم يستعملها، أما الخانات البيضاء فإنها فارغة قابلة للاستعمال.
لنفترض أنك تود إضافة مهمة رابعة إلى الصفيفة، لكنك لن تقدر على ذلك لأن الخانة المجاورة مستعملة، أحدهم أخذها قبلك!
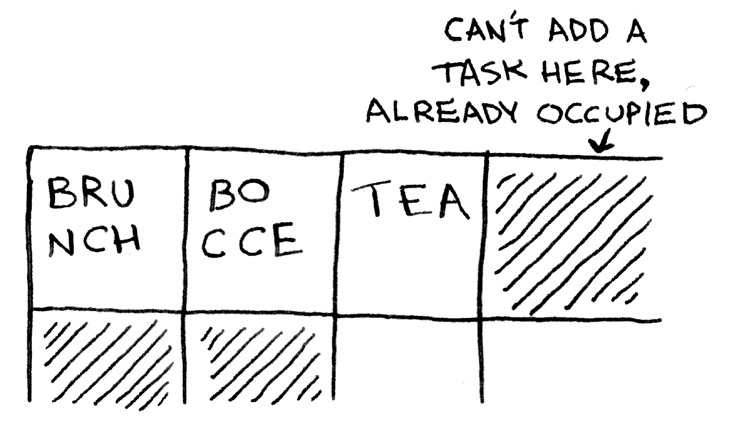
ولأجل إضافة مهمة رابعة ستطلب من الحاسوب مكان مختلف في الذاكرة لتخزين أربع مهام متجاورة، أي ستطلب من عبود أربعة أدراج متجاورة، وسينقل لك عبود الثلاث المهام السابقة إلى الخانات الجديدة مع إضافة المهمة الجديدة.
هذا يشبه أن تتفق مع الأصدقاء لمشاهدة مسرحية، فيتأخر بعضهم فتذهبَ لمشاهد المسرحية مع الحاضرين، وتبحثون عن كراسي متجاورة للجلوس معًا، وثم لما يأتي صديق جديد متأخر لا يعثر على كرسي للجلوس معكم فإنكم تنهضون جميعًا وتبحثون عن كراسي متجاورة لكم جميعًا، ونِعمَ الصداقة!
افترض أن صديقًا جديدًا أتى، فهل تنهضون مرة أخرى للبحث عن مكان آخر لكم جميعًا؟ ماذا لو تكرر الأمر أكثر من مرة؟ أتنهضون؟
لا بلا ريب، فهذا ليس حلًا عقلانيًا. وبالمثل فإن إضافة عنصر كل مرة إلى الصفيفة ليس حلًّا جيدًا، وهو بطيئ جدًا.
لنفترض أنك فكرت بحل لها وقلت: سأحجز كراسي متجاورة لنا جميعًا، بل سأحجز أكثر من عددنا لعل صديقًا يأتي معنا لاحقًا!
وبالمثل فأنك ستنشئ صفيفة حجمها عشرة، لعلَّك تخزن مهمة جديدة، فتطلب من الحاسوب حجز عشر خانات في الذاكرة لهذه الصفيفة. لهذا الحل مساوئ:
1. تلك الكراسي قد لا تستعملها، وبالمثل قد لا تستعمل تلك الخانات التي حجزتها في الذاكرة، ولن تدع غيرك يستعملها، فضاعت هباءً منثورًا.
2. قد تحتاج إلى كراسي أكثر مما حجزت، فتضطروا لأن تنهضوا وتبحثوا عن كراسي أخرى، وبالمثل قد تخزن أكثر من عشر مهام، فتضطر إلى طلب عدد خانات متجاورة أكثر في مكان آخر.
الحل الذي فكرت به جيد وتُشكَرُ عليه، لكن به ثغور خطيرة، والحل استعمال اللائحة المترابطة.
اللائحة المترابطة linked list
باستعمال اللائحة المترابطة فإن العنصر يمكن أن يكون في أي مكان في الذاكرة!
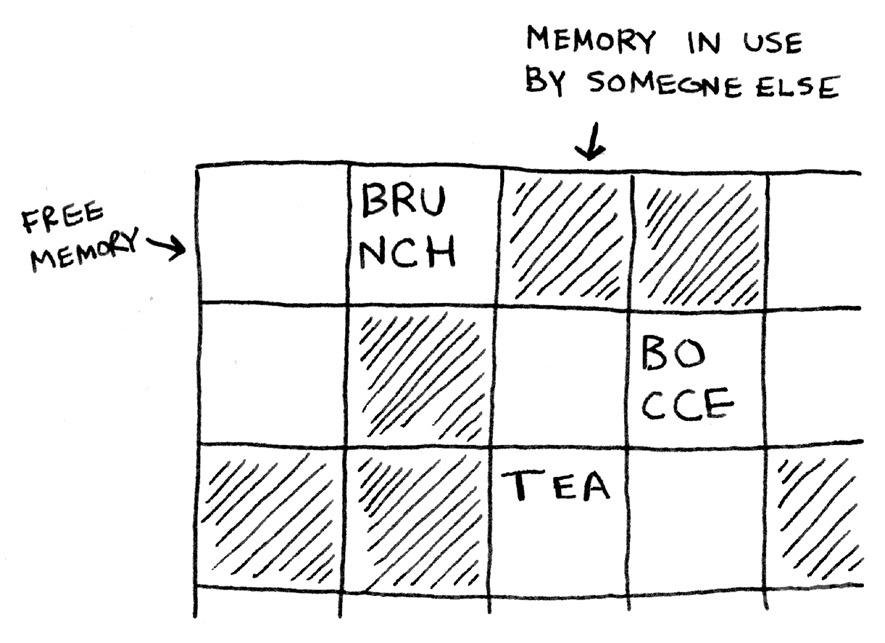
ما يميزها أن كل عنصر يشير إلى مكان العنصر الذي يليه في الذاكرة. القائمة المترابطة مجموعة من عناصر، كل عنصر يشير إلى مكان العنصر الذي يليه في الذاكرة، فكل عنصر يحمل عنوان (مؤشر pointer) العنصر الذي يليه.
في بعض المراجع يسمى العنصر بالعقدة node، فإن كل عقدة تحمل عنوانًا يشير إلى العقدة التي تليها.
انظر إلى هذه الأسهم الخارجة من العنصر الأول إلى العنصر الثاني، ومن العنصر الثاني إلى العنصر الثالث، فجميعها مترابطة:
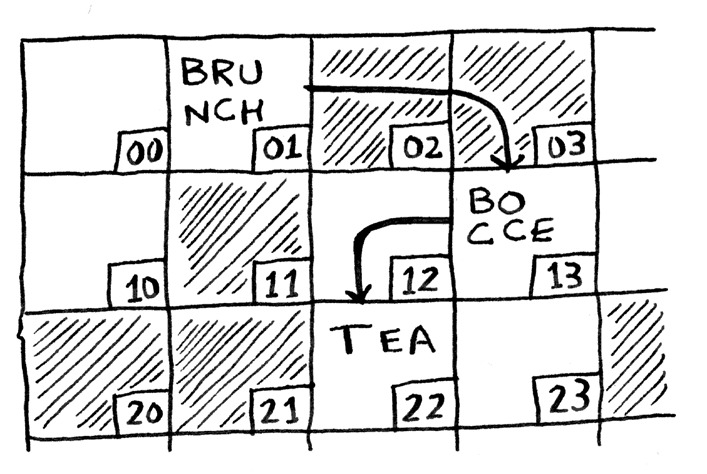
اللائحة المترابطة تشبه التلميحات أو الخيوط التي توصلك للكنز، تذهب إلى المكان الفلاني فتجد خيطًا يوصلك إلى مكانٍ آخر فيه خيط جديد، فكل خيط يقربك من العثور على الكنز، فجميع الخيوط مترابطة، وفي النهاية تعثر على الكنز!
إضافة عنصر إلى اللائحة المترابطة سهل جدًا، تخزن أي عنصر في أي مكان في الذاكرة، ثم تأخذ عنوانه وتعطيه للعنصر الذي يسبقه، ليشير العنصر السابق إلى العنصر الجديد. وباستعمال اللائحة المترابطة لن تضطر أبدًا إلى نقل عناصرك كل مرة إلى موضع جديد.
باستعمالك اللائحة المترابطة فقد تنجبت من مشكلة، أتعلم ما هي؟
افترض أنك ستذهب إلى لمشاهدة مسرحية مع خمسة أصدقاء، وعندما وصلتم لم تجدوا إلا خمسة كراسي متجاورة، فالمسرح ممتلئ وليس فيه أكثر من خمسة كراسي متجاورة فبقيتها منفصلة، وثم فجأة جاء صديق سادس إليكم. في هذه الحالة لا تستطيعون أن تنتقلوا إلى مكان آخر، فالمسرح ممتلئ.
وبالمثل الصفيفة، فإن لم تجد مساحة لتخزين ألف ألف عنصر في خانات متجاورة في الذاكرة فلا يمكنك إنشاء الصفيفة، وهذه مشكلة عويصة!
اللائحة المترابطة تحل المشكلة، فإنها تشبه أن تقول للأصدقاء: للنفصل ونشاهد المسرحية، كل منا في كرسي منفصل!
إن كانت في الذاكرة مساحة فارغة فأنك قادر على إنشاء لائحة مترابطة، لا حاجة لأن تكون العناصر متجاورة.
إن كانت اللائحة المترابطة أفضل في إدخال عناصر جديدة فما فائدة الصفيفة؟
لنعود إلى الصفيفة!
الصفيفة والبحث عن عنصر
تستعمل بعض المواقع التي تستعرض أفضل عشرة كتب أو مسلسلات حيلة لعينة لوضع إعلانات كثيرة، ينشئون صفحة وعليها الكتاب التاسع، ولكي ترى الكتاب الذي يليه تضغط على زر “التالي”، لتظهر لك صفحة جديدة عليها كتاب واحد فقط، ولكي ترى الكتاب الأول عليك أن تمر بتسع صفحات مليئة بالإعلانات!
أليس من الأفضل أن يضعوا صفحة واحدة وعليها أسماء جميع الكتب، ولمن أراد قراءة معرفة معلومات عن أي كتاب يكفه أن يضغط على اسم الكتاب ليذهب إلى الصفحة المقصودة؟
اللائحة المترابطة بها سيئة، إنها تشبه المواقع التي تستعرض عشرة كتب في عشر صفحات، ولكي ترى الكتاب التالي عليك الضغط على زر “التالي”، فلا يمكنك الذهاب إلى آخر عنصر إلا بالمرور على جميع العناصر التي تسبقه!
هذه سيئة في اللائحة المترابطة، للذهاب إلى عنصر في اللائحة عليك المرور بالعناصر التي تسبقه، لأنك لا تعلم أين يُخزَّن في الذاكرة، فتتبع عنوانه، مثل الخيوط الموصلة للكنز!
تتفوق الصفيفة على اللائحة المترابطة في هذه الحالة، فأنت تعرف عنوان كل عنصر في الذاكرة.
افترض أن لديك صفيفة من خمسة عناصر، وأنت تعلم أن أول عنصر يبدأ من العنوان 00، فما عنوان العنصر الأخير يا ترى؟
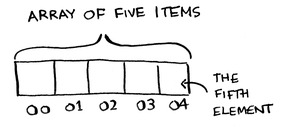
عنوانه 04!
الصفيفة فعالة للبحث عن عنصر عشوائي أما اللائحة المترابطة فلا، لأن العناصر غير متجاورة، وللبحث عن عنصر عليك المرور بكل عنصر يسبقه، فلا تعلم في أي خانة يخزن العنصر!
الدليل
إن كنت تتساءل لماذا بدأنا العد في الصفيفة السابقة من الرقم صفر، فيحزنني هذا التساؤل، فأنك لم تدرس لغة البرمجة جيدًا!
العناصر في الصفيفة مرقَّمة، يبدأ الترقيم فيها من الرقم صفر لا الواحد. انظر إلى هذه الصفيفة من سبعة عناصر هي -على التوالي- 21 و13 و42 و7 و19 و27 و45.
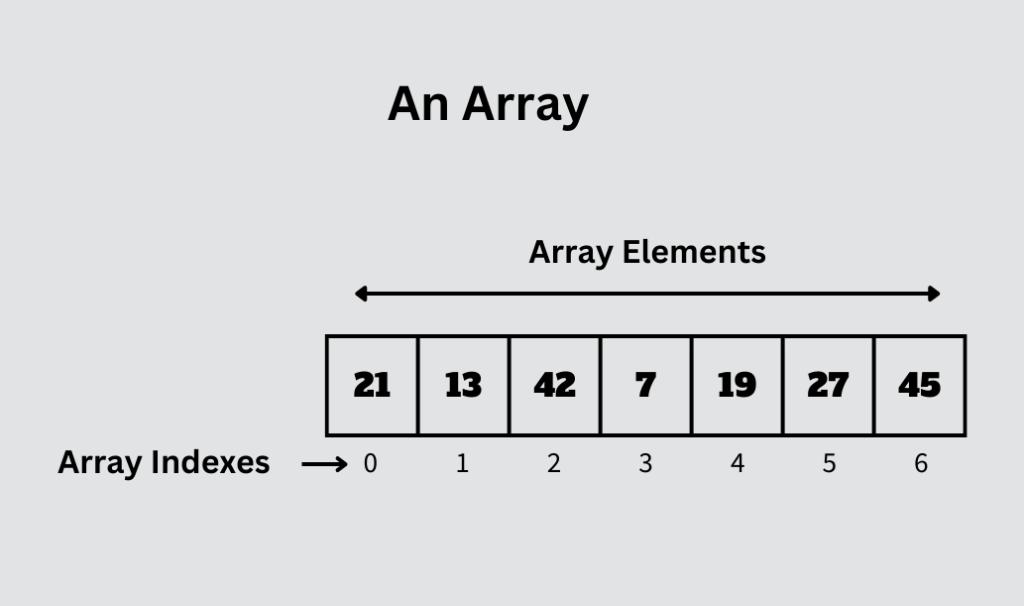
العنصر الثاني 13 موضعه واحد لا اثنين، فنحن لا نبدأ العد من الرقم واحد في لغات البرمجة، بل من الصفر. وهذا يسمى بالدليل index (حسب قاموس الجمعية السورية للمعلوماتية). وهذا الدليل قيمة تمكنك من النفاذ المباشر إلى عنصر في الصفيفة.
من الآن وصاعدًا سأستعمل لفظة دليل index للإشارة إلى موضع العنصر في الصفيفة أو اللائحة المترابطة.
تعقيد الوقت
حان وقت استحضار الدروس السابقة، تحديدًا درس تعقيد الوقت ورمز O الكبير!
سنعرف تعقيد الوقت للعمليتي قراءة العناصر reading وأدراجها inserting لكل من القائمة المترابطة والصفيفة.
تعقيد الوقت لعملية القراءة للصفيفة يساوي (1)O، أما لعملية الأدراج (س)O.
تعقيد الوقت لعملية القراءة للائحة المترابطة (س)O، أما لعملية الأدراج (1)O.
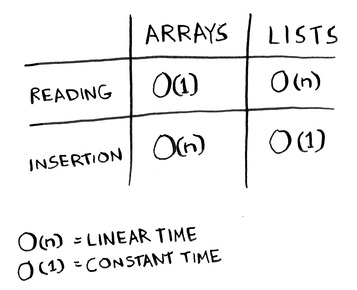
الوقت الخطي (س)O
الوقت الثابت (1)O
تمرين مباغت
افترض أنك برمجتَ بُريمجًا لمراقبة مقدار ما تصرف. وكل يوم تدون ما أنفقته، وفي نهاية الشهر تراجع ما أنفقته وتحسب مقدار المال الذي جمعته. إذن فإن لديك الكثير من مرات الأدراج والقراءة، فهل تستعمل اللائحة المترابطة أم الصفيفة؟
أدراج عنصر إلى الوسط
افترض أنك تريد أن تكون قائمة مهامك مثل التقويم، فسابقًا تعرفنا على إضافة عنصر إلى نهاية اللائحة أما الآن سنتعرف على أدراج عنصر إلى الوسط.
حاليًا ترغب أن تكون قائمة مهامك مثل التقويم لتكون العناصر غير المرتبة unordered مرتبة ordered.
فهل ستستعمل اللائحة المترابطة أم الصفيفة؟
يسهل تغيير العنوان الذي يشير إليه العنصر السابق. انظر إلى هذه الصورة:
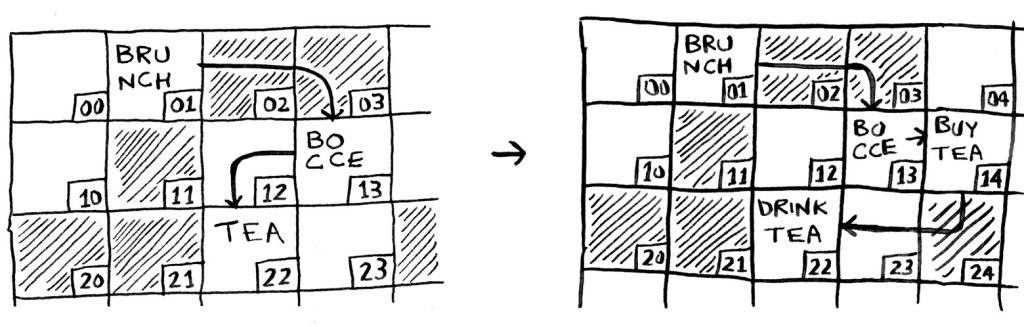
لكن في الصفيفة عليك إزاحة shift العناصر التي تلي الدليل index بمقدار خطوة لأدراج عنصر واحد، ولو لم تتوافر مساحة في الذاكرة ستضظر لنقل الصفيفة إلى مكان آخر.
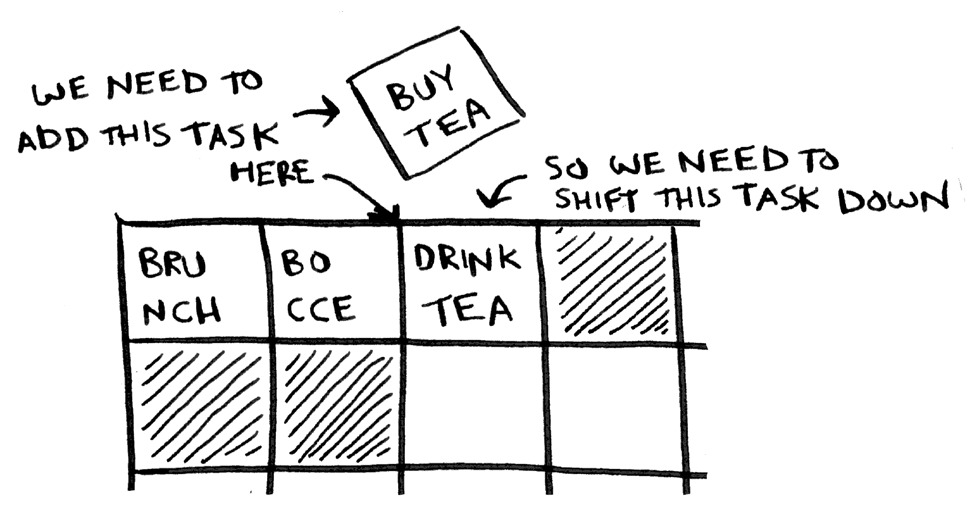
فكما ترى فإن اللائحة المترابطة أفضل لأدراج عنصر إلى منتصف اللائحة.
ماذا عن حذف عنصر يا مبعسس؟ هل اللائحة المترابطة أم الصفيفة أفضل؟
نرغب بحذف عنصر من اللائحة!
على رسلكم، سنتحدث عن الحذف ومعرفة تعقيد الوقت في حذف عنصر لكلا اللائحة المترابطة والصفيفة.
حذف عنصر
ترغب بحذف عنصر؟
أستفكر لمعرفة الحل أم أقول لك، ها؟ ها؟
فكرت أم لا؟
حسنًا، سأخبرك، اللائحة المترابطة أفضل في الحذف أيضًا، لأنك ستغير العنوان الذي يشير إليه العنصر السابق فقط.
نفترض أنك ترغب بحذف العنصر س، والعنصر الذي يسبق العنصر س هو ص، وأنت تعلم أن العنصر ص يشير إلى عنوان العنصر س، لذا نحذف العنصر س، ونغير العنوان الذي يشير إليه العنصر ص إلى العنصر الجديد.
الحذف سيعمل دائمًا بعكس الإدراج، فالإدراج قد يفشل لعدم مساحة في الذاكرة.
انظر إلى الصورة التالية، فتعقيد الوقت في حذف عنصر في الصفيفة (س)O، أما في اللائحة المترابطة O(1).
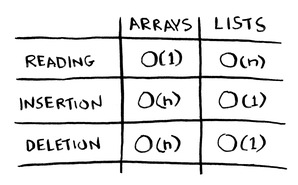
لكن لماذا O(1) في حذف عنصر من اللائحة المترابطة؟
هذا يكون في حالة خاصة، بأن تكون عارفًا بمكان العنصر الذي ستحذفه، ويتم هذا الأمر بمعرفة العنصر الأول في اللائحة والعنصر الأخير، فالأمر في هذه الحالة ثابت، أي O(1).
الصفيفة أم اللائحة المترابطة؟
بوصولك إلى هذه المرحلة فأنك قادر على الجواب، فإن الأمر يعتمد على حالة الاستعمال التي ترغب بها، فقد قارنا بين الصفيفة واللائحة المترابطة من قراءة وأدراج وحذف. الصفيفة سريعة في القراءة، سريعة في النفاذ إلى عنصر عشوائي!
سنرى في الفصول التالية من الكتاب استعمال الصفيفة واللائحة المترابطة لإنشاء بُنى معطيات data structures.
التمارين
1. نفترض أنك تبني تطبيق لمطعم لتلقي الطلبات من الزبائن. تطبيقك يحتاج لتخزين لائحة من الطلبات. النُدُل (جمع نادل) يستمرون بإضافة الطلبات إلى هذه اللائحة والطهاة يقرأون هذه الطلبات من اللائحة ويطبخ للزبائن.
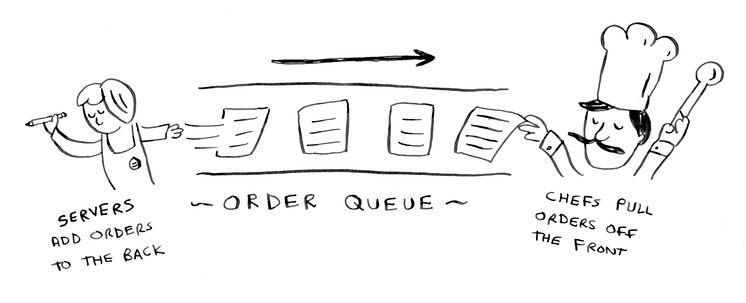
فالسؤال: هل ستستعمل اللائحة المترابطة أم الصفيفة؟
تلميح: اللائحة المترابطة ممتازة لأدراج وحذف العناصر، والصفيفة ممتازة للنفاذ إلى عنصر عشوائي.
2. لنفترض أن فِيسبُك يستعمل خوارزمية البحث الثنائي (التي سبق شرحها هنا)، ولنفترض أنه يخزن أسماء المستخدمين في لائحة. إذا حاول شخص ما الولوج إلى فِيسبُك فإنه يبحث عن اسم مستخدم الشخص في اللائحة.
إن كان اسم المستخدم في اللائحة = يلج المستخدم لفِيسبُك. كثير من الأنام يحاولون الولوج إليه، لذا فإن فِيسبُك يجري عمليات بحث كثيرة يوميًا.
خوارزمية البحث الثنائي ستصل إلى منتصف اللائحة سريعًا. إذن هل ستستعمل اللائحة المترابطة أم الصفيفة؟
3. لنفترض أنك استعملتَ الصفيفة لحل التمرين السابق، فما مساوئ استعمال الصفيفة لأدراج مستخدمين إليها بافتراض أن الناس أرادوا التسجيل في الموقع (إنشاء حساب)، وأردت إضافة المستخدمين الجُدد إلى الصفيفة؟
4. حقيقةً الفِيسبُك لا يستعمل صفيفة أو لائحة مترابطة لتخزين المستخدمين، بل بنية معطيات هجينة: صفيفة من اللوائح المترابطة.
الصفيفة مكونة من 29 خانة، كل خانة تشير إلى لائحة مترابطة. مثلًا تشير الخانة الأولى في الصفيفة تشير إلى لائحة مترابطة تحوي جميع أسماء المستخدمين الذين يبدأ اسمهم بحرف الألف A، والخانة الثانية تشير إلى لائحة مترابطة تحوي جميع أسماء المستخدمين الذين يبدأ اسمهم بحرف الباء B، وهكذا…
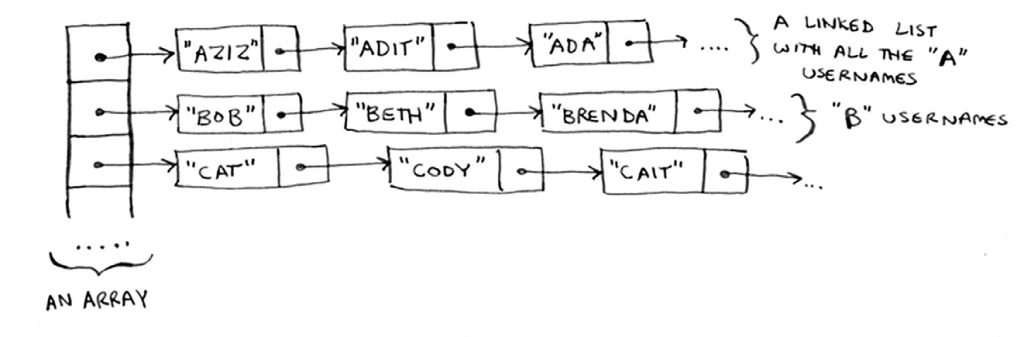
لنفترض أن أحمد سجل في الفِيسبُك، لذا ستضيفه إلى اللائحة، فتذهب إلى الخانة الأولى، فتجدها تشير إلى اللائحة المترابطة التي تحوي جميع أسماء المستخدمين الذين يبدأ اسمهم بحرف الألف، وتضيف أحمد إلى نهاية اللائحة.
لنفترض أنك تبحث عن اسم يوسف عبد العزيز، فتذهب إلى الخانة الأخيرة 29، التي تشير إلى اللائحة المترابطة التي تحوي على جميع أسماء المستخدمين الذين يبدأ اسمهم بحرف الياء، وتبحث عن اسمه هناك.
قارن بنية المعطيات الهجينة هذه باللائحة المترابطة والصفيفة، هل هي أبطأ أم أسرع في كل من البحث والأدراج؟
ليس من الضروري إيجاد تعقيد الوقت لها، رمز O الكبير، مناط بك تحديد أهي أسرع أم أبطأ فقط.
خذ وقتك في حل التمارين، يجب عليك حلها كاملةً!
الخاتمة
ها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.