كتاب استيعاب الخوارزميات -الفصل الثاني، الدرس الأخير- خوارزمية الفرز بالانتقاء

السلام عليكم ورحمة الله تعالى وبركاته، هذا الدرس الأخير في الفصل الثاني من كتاب «استيعاب الخوارزميات Grokking Algorithms»، الذي سبق وشرحنا الدرس الأول منه وعنوناه «اللائحة المترابطة والصفيفة».

سنتعلم اليوم أول خوارزمية فرز، خوازرمية الفرز بالانتقاء، بعد أن تعلمنا أول خوازرمية بحث لنا، خوازرمية البحث الثنائي، في الفصل الأول.

خوارزمية الفرز بالانتقاء

خوارزمية الفرز بالانتقاء selection sort، خوارزمية سهلة لترتيب العناصر، سهلة كسهولة خوارزمية البحث الثنائي.
الفاء والرَّاء والزاي في اللغة تدل على عزل الشيء عن غيره، وهي مجموعة في كلمة فرز، وجاء في لسان العرب: “فَرَزْتُ الشيء أَفْرِزُه إِذا عزلته عن غيره ومِزْتَه”، وكلمة انتقاء تعني اختيار.

إذن اسمها يدل على فرز شيء، أي عزله من شيء، لترتيبه بالانتقاء، أي بالاختيار.

خوارزمية الفرز بالانتقاء تفرز (تعزل) أصغر عنصر في اللائحة، أي أنها تفرز العناصر بانتقاء أصغر عنصر في اللائحة، مرارًا وتكرارًا حتى تترتب العناصر جميعًا.

تبحث الخوارزمية عن أصغر عنصر في اللائحة، بمقارنة أول عنصر بالعنصر الذي يليه وهكذا…

ولما نجد أصغر عنصر نضعه في بداية اللائحة، ونكرر الأمر لبقية العنصر لنجد العنصر الذي يلي أصغر عنصر في الصِغَرِ في اللائحة.

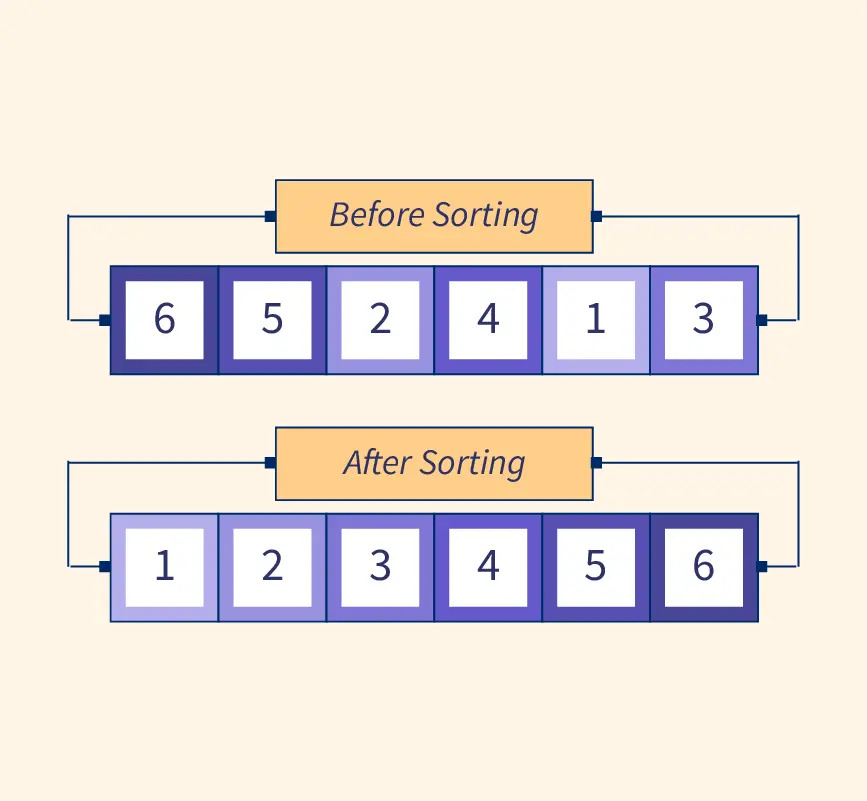
بمعرفتنا بكيفية عملها نستنتج أن الخوارزمية ستُقَسِّم اللائحة إلى جزئين، جزء مفروز sorted وجزء غير مفروز unsorted، وسيكون عمل الخوارزمية في الجزء غير المفروز، وستستمر بالبحث عن أصغر عنصر في الجزء غير المفروز.

في بداية عمل الخوارزمية فإن اللائحة تكون غير مفروزة، وثم يظهر الجزء المفروز، ورويدًا رويدًا سيتناقص الجزء غير المفروز ويزداد الجزء المفروز.

إن كنت تتساءل لماذا أصغر عنصر فذلك لأننا سنرتبها تصاعديًا، أما إذا أردنا تنازليًا فسنفرز أكبر عنصر…

مثال نظري

افترض أن لديك لائحة من الأغاني على حاسوبك، مكتوب بجانب كل أغنية عدد المرات التي سمعتها به، وترغب بمعرفة أكثر أغنية تستهلك وقتك لحذفها، واستبدالها بسورة من القرآن الكريم. انظر:

إحدى الطرائق لمعرفة ذلك أن تبحث عن أكثر أغنية استمعتَ لها، ثم تضعها في لائحة جديدة.

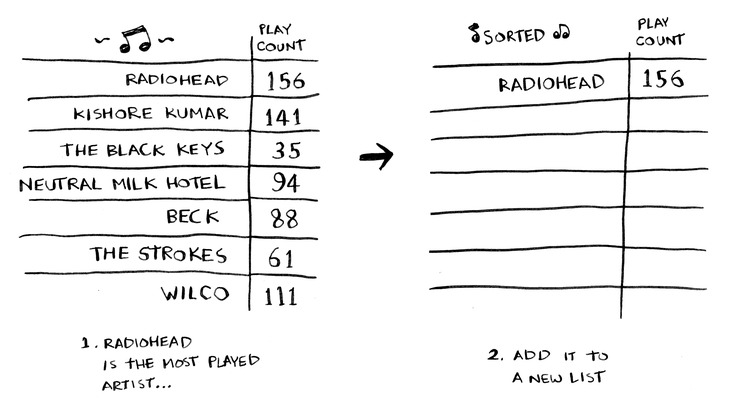
ثم تبحث عن الأغنية التي تلي الأولى في عدد مرات الاستماع، وتضيفها إلى اللائحة السابقة.

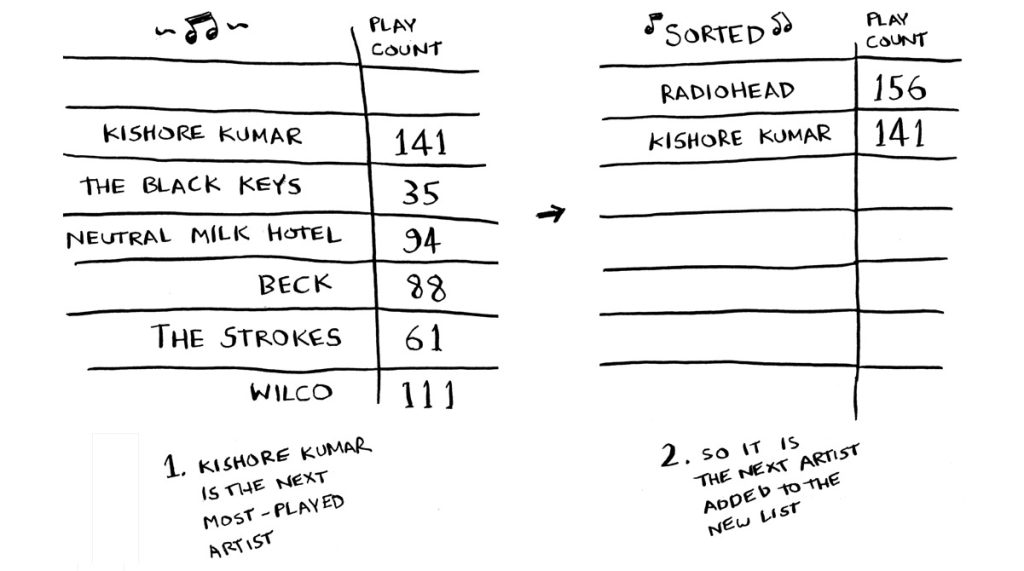
وتكرر العملية حتى تترتب كل الأغاني تنازليًا.

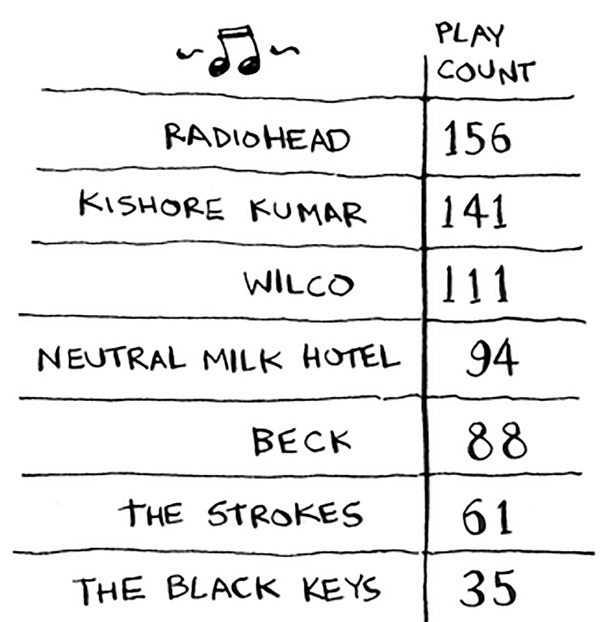
تعقيد وقت الخوارزمية

لنلبس رداء المبرمج الفذ ونرى ما رمز O الكبير لها. في الدرس الثاني من الفصل الأول، درس «تعقيد الوقت ورمز O الكبير»، عرفنا أن (س)O يعني المرور على كل عنصر في اللائحة مرة واحدة.

إذا استعملنا خوارزمية البحث الخطي، التي درسناها في الدرس الأول من الفصل الأول، فإنها ستمر على كل عنصر في اللائحة مرة واحدة.

خوارزمية البحث الخطي ستمر على جميع العناصر مرة واحدة، فإذا كانت اللائحة مكونة من س عنصر، فإن رمز O الكبير لها لإيجاد أصغر عنصر هو (س)O.

ولإيجاد العنصر الذي يلي العنصر الأول في الصِغَرِ فإن رمز O الكبير لها هو (س)O، وهكذا سنستمر بفعل نفس الشيء…

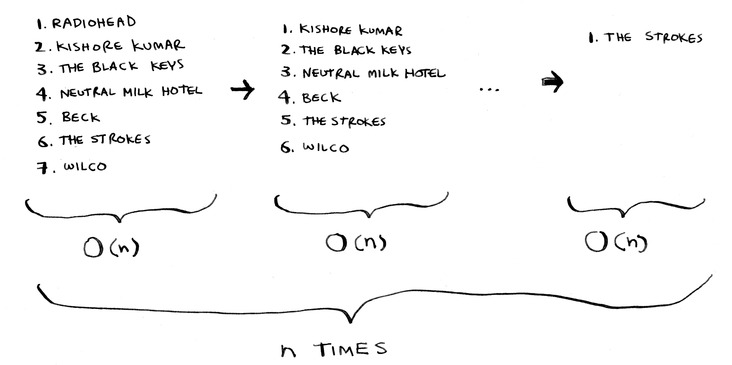
إذن في رمز O الكبير النهائي سيكون (س×س)O، أي ضرب طول اللائحة في نفسه، والذي يساوي بصيغة أخرى (س²)O، أي س تربيع، والذي يعني ضرب العدد في نفسه.

انتظر انتظر يا مبعسس، أظنك أخطأت!
أليس عدد العناصر الذي تمر عليها خوارزمية الفرز بالانتقاء تتناقص كل مرة تفرز فيها عنصرًا؟

أحسنتَ، ليس عليك التحقق من جميع العناصر كل مرة، سيتناقص العدد تدريجيًا، إن فرزت العنصر الأول، فإن حجم الجزء غير المفروز ينقص واحدًا، وإن فرزت العنصر الثاني فإن الجزء غير المفروز سينقص عنصرين.

يمكننا تمثيل هذا رياضيًا بما يسمى بالمتسلسلة الحسابية، هكذا:
(س-١) + (س-٢) + … + ٢ + ١
ومجموع المتسلسلة الحسابية يختصر إلى المعادلة التالية:
س(س-١)/٢
أي، س ضرب (س-١) قسمة ٢.

إذن لماذا قلت أن تعقيد الوقت (س²)O؟

السبب له علاقة بالثوابت، سنناقشه في الفصل الرابع وليس الآن، لكن سأشرح لك المفهوم فقط وثم سنناقشه في الفصل الرابع.
بحسب المتسلسلة الحسابية السابقة فإننا في المتوسط سنحسب عدد عناصر قدرهم س×١/٢ عنصرًا. إذن فإن رمز O الكبير لها (س × ١/٢ × س)O.

لكن الثابت مثل ١/٢ يُحذفَ ولا يُعبأ به في رمز O الكبير، فيصبح رمز O الكبير لها (س × س)O، وهو نفسه (س²)O.

إن لم تفهم فأعد قراءة الفقرة مرة ثانية، وإن لم تفهم فأعد قراءة الفقرة في وقتٍ لاحق في مكان هادئ، وإن لم تفهم أيضًا فأنك ستفهم لاحقًا عند وصولنا الفصل الرابع!

خلاصة عمل الخوارزمية:
١. نجعل العنصر الأول في اللائحة أصغر عنصر.
٢. نقارن العنصر الذي يلي في اللائحة إن كان أصغر منه نجعل العنصر الجديد العنصر الأصغر في اللائحة بدلًا من العنصر السابق.
٣. نستمر بتطبيق الخطوة الثانية لجميع عناصر اللائحة حتى ننتهي من كل عنصر.
٤. عند الانتهاء من التحقيق من كل عناصر اللائحة = نستبدل أول عنصر باللائحة بأصغر عنصر عثرنا عليه.
٥. نكرر الخطوات من واحد إلى أربعة حتى ننتهي من كل عناصر اللائحة غير المفروز.

مبارك عليك تعلم خوارزمية الفرز الأولى لك!
الآن تقدر على ترتيب الأسماء في قاعدة البيانات وترتيب البريد الرقمي من الأحدث إلى الأقدم، وفعل الكثير!

هذه الخوارزمية قد لا تكون فعالة للائحة ضخمة، لكنها أسهل في التطبيق لمن لا تهمه السرعة أو الكفاءة في لائحة ضخمة، لكنها مفيدة لعناصر قليلة.

مثال نظري ثانٍ

لدينا قائمة من عناصر: ٨، ٥، ٢، ٦، ٩، ٣، ١، ٤، ٠.

سنستعمل خوارزمية الفرز بالانتقاء لترتيب كل هذا العناصر تصاعديًا. عندما تعمل الخوارزمية سترى مربع الرقم يتحول إلى اللون الأزرق، وهذه أمارة على أن الخوارزمية تعمل على هذا الرقم.

إن كان الرقم صغيرًا فإن مربع الرقم سيتحول للون الأحمر، وهذه أمارة على أنه أصغر رقم عثرت عليه الخوارزمية.

وعندما تنتهي الخوارزمية من العثور على أصغر عنصر والتحقق من كل عناصر اللائحة فإن الرقم الصغير سيكون أول رقم في اللائحة، وسيتغير لونه إلى اللون الأصفر.

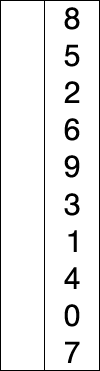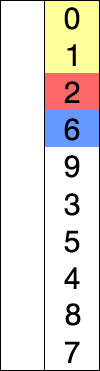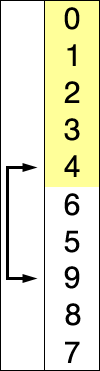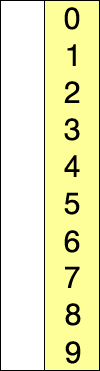
وهكذا تستمر الخوارزمية حتى ترتب جميع العناصر، كما ترى في هذه الصورة المتحركة!

التمرين والمثال عملي

الآن عندنا تمرين حقيقي يختبر فهمنا، وهو مثال عملي أيضًا، سنحل مسألة على موقع codeforces، وهو موقع يقدم مسائل برمجية للمبرمجين، تحديات لتنمية مهارة حل المسائل problem solving.

اسم المسألة جاذبية فليپ Gravity Flip الموسومة بوسم الفرز، وخلاصتها أن ولدًا ضجر من دراسة درس الفيزياء في غرفته، فبنى صندوقًا يغير جاذبية الأشياء داخله بالضغط على زر فيه.

يحتوي الصندوق على س أعمدة، في كل عمود س من المكعبات، عند الضغط على زر الجاذبية تتوجه المكعبات نحو الجهة اليمنى من الصندوق.

الشكل التالي يوضح المكعبات بعد الضغط على زر الجاذبية، وقد مُيَّزت المربعات التي تغير موضعها باللون البرتقالي.

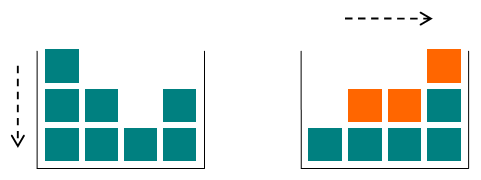
ما تطلبه المسألة أن تظهر عدد المربعات في كل عمود بعد الضغط على زر الجاذبية.

المدخلات: عدد الأعمدة، وعدد المكعبات في كل عمود. وعدد الأعمدة أو المكعبات في كل عمود لن يتخطى حاجز المائة صندوق.

سنمثل الصورة السابقة برمجيًا. المدخلات:

٤
٢ ١ ٢ ٣

المخرجات:
١ ٢ ٢ ٣

وهذا مثال آخر:
٣
٢ ٣ ٨
المخرجات:
٢ ٣ ٨

بحسب ما سبق، وبدرس اليوم فإن حل المسألة واضح جلي للعيان. عليك حل المسألة قبل رؤية الحل، حلها بلغة البرمجة التي تجيدها، فلا مندوحة لك عن حلها!

سنحل المسألة بلغة الثعبان python:

# Finds the smallest value in an array
def findSmallest(arr):
  # Stores the smallest value
  smallest = arr[0]
  # Stores the index of the smallest value
  smallest_index = 0
  for i in range(1, len(arr)):
    if arr[i] < smallest:
      smallest_index = i
      smallest = arr[i]      
  return smallest_index

# Sort array
def selectionSort(arr):
  newArr = []
  for i in range(len(arr)):
      # Finds the smallest element in the array and adds it to the new array
      smallest = findSmallest(arr)
      newArr.append(arr.pop(smallest))
  return newArr
OurList = []
n = int(input())
for i in range(1,n):
    tem = int(input())
    OurList.append(tem)
print(selectionSort(OurList))

وهذا حل بلغة C:

#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

// Finds the smallest value in an array
int findSmallest(int *arr, int size) {
    // Stores the smallest value
    int smallest = arr[0];
    // Stores the index of the smallest value
    int smallest_index = 0;
    for (int i = 1; i < size; i++) {
        if (arr[i] < smallest) {
            smallest = arr[i];
            smallest_index = i;
        }
    }
    return smallest_index;
}

int *selectionSort(int *arr, int size) {
    // Create new Array
    int *newArr = (int *)malloc(size * sizeof(int));
    for (int i = 0; i < size; i++) {
        int smallest = findSmallest(arr, size);
        newArr[i] = arr[smallest];
        // same as deleted by changing to the largest value
        arr[smallest] = INT_MAX;
    }
    return newArr;
}

int main(void) {
    int size;
    scanf("%d", &size);
    int arr[size];
    for (int i = 0; i < size; i++) {
        scanf("%d", &arr[i]);
    }
    int *sortarr = selectionSort(arr, size);
    // print result
    for (int i = 0; i < size; i++) {
        printf("%d ", sortarr[i]);
    }
    return 0;
}

الخاتمة

ها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.

وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.