السلام عليكم ورحمة الله تعالى وبركاته
هذا الدرس الأول من الفصل الرابع من كتاب استيعاب الخوارزميات، الذي سبق ونشرنا آخر مقال منه بعنوان «كتاب استيعاب الخوارزميات -الفصل الثالث، الدرس الأخير- الكَدسَة».
ولتفهم درس اليوم فعليك فهم الدروس السابقة، وخاصة درس العَوْدِيَّة، لأن الدروس الحالية ستبنى على ما قد شُرِحَ.
فرق تسد

سياسة فَرِّق تَسُد سياسة قديمة طبقها اليونانيون والسومريون لتفكيك قوى العدو إلى قوى أصغر، وهي سياسة مستعملة في الحروب، إذ تهدف إلى تمزيق وتشتيت قوى العدو سواء بزرع الشقاق والخلاف بينهم أو غيره، وبعد التفريق بينهم يسهل التعامل من الجماعات المتفرقة وإخضاعها، وهكذا يسود عليهم!
في الاجتماع قوة، فرقهم تسد عليهم، شتت بشملهم يسهل إخضاعهم. قد طبقت هذه السياسة في اتفاق سايكس وبيكو الملعونان التي هدفت لتقسم الوطن العربي إلى دول منفصلة لها شعارها وحدودها المقدسة للحيلولة دون قيام اتحاد عربي قوي لأن اتحاد العرب يخيفهم!
سنستعمل هذا المفهوم في الخوارزميات، لأن بعض المسائل لا تُحَل بأي خوارزمية درستها، ولا بد أن يكون هذا المفهوم ضمن عُدَّة المبرمج، فالمبرمج عنده عُدَّة يستعملها عند كل مسألة يواجهها، وعندنا في علم الحاسوب خوارزميات كثيرة تندرج تحت مفهوم فرق تسد divide and conquer، وسنتعلم بعد هذا المنشور أول خوارزمية تندرج تحت مفهوم فَرِّق تَسُد، وهي خوارزمية فرز.
بتطبيق هذا المفهوم على مسألة عندنا، لنقل إنها المسألة “أ”، ستقسم المسألة إلى مسائل أصغر يسهل حلها، لنقل “ب” و”ج”، وإن اقتضى الأمر قسمنا المسائل التي سبق تقسيمها إلى مسائل أصغر أيضًا ليسهل حلها، ونستمر بالتقسيم وحل المسائل الفرعية حتى تصل المسألة إلى أصغر جزء ويكون في هذه الحالة الجزء محلول.
وكما ترى أننا طبقنا مفهوم العَوْدِيَّة عند استعمال مفهوم فرق تسد، إذ قسمنا المسألة الكبيرة الأساسية إلى مسائل فرعية أصغر، وفي كل مرة نستمر في التقسيم وحل المسائل الفرعية حتى نصل لمرحلة معينة نتوقف عندها.
الخوارزميات المندرجة ضمن تصنيف فَرِّق تَسُد خوارزميات عَوْدِيَّة recursive algorithm!
أعد قراءة ما قلته إن لم تفهمه، وإن لم تفهمه فهذا مثال عملي سنتطبق عليه مفهوم فرق تسد.
المثال الأول
أتدري؟
صاحبنا عبود أصبح مزارعًا!
يريد مِنَّا أن نساعده في مسألة نغصت حياته، كما قال.
لدى المزارع عبود قطعة أرض، مزرعة، عرضها ١٦٨٠ مترًا وطولها ٦٤٠ مترًا.
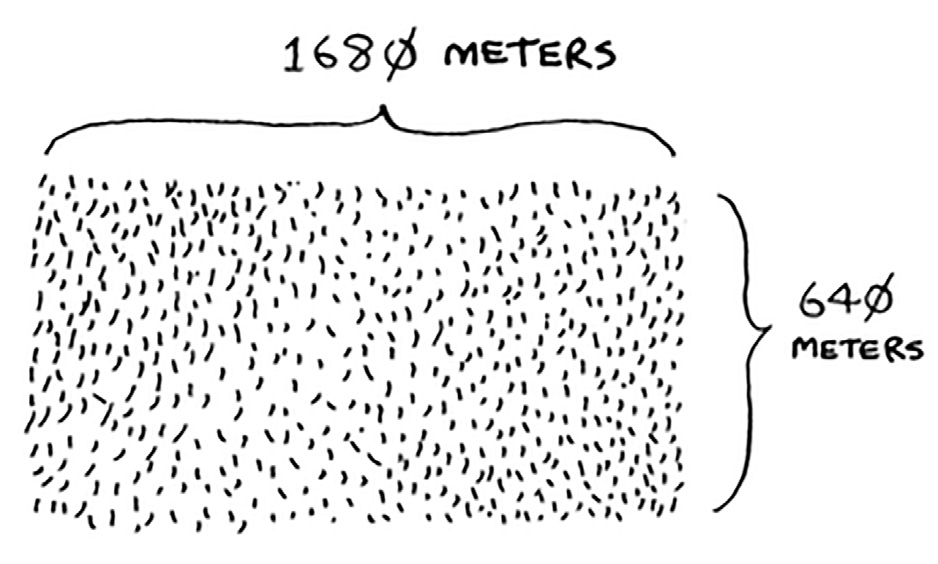
يريد أن يقسم المزرعة بالتساوي إلى قطع مربعة أصغر، أي كلها بنفس الحجم، وتكون كبيرة بقدر المستطاع. لنساعد عبود لفعل ذلك. ماذا سنفعل؟
لنستعمل سياسة فَرِّق تَسُد!
كما سبق وقلت، الخوارزميات المندرجة ضمن تصنيف فَرِّق تَسُد خوارزميات عَوْدِيَّة، لذا لمساعدة عبود فعندنا خطوتين سننفذها:
١. نحدد جزء التوقف base case، وهي النقطة التي سنتوقف عندها. راجع درس العَوْدِيَّة لتفهم أجزاء العَوْدِيَّة.
٢. نفرق أو نقسم المسألة حتى نصل إلى جزء التوقف الذي حددناه في الخطوة الأولى.
لنستعمل سياسة فَرِّق تَسُد لنحل المسألة ونساعد صاحبنا عبود. ما أكبر حجم مربع يقدر عبود على استعماله في أرضه وتكون أرض عبود مقسمة إلى مربعات متساوية الحجم؟
لنحدد جزء التوقف أولًا. سيكون جزء التوقف في هذه الحالة: عرض الأرض ضعف طولها، مثلًا لو أن عرض الأرض خمسين مترًا سيكون طولها خمسة وعشرين مترًا، بحيث لا تبقى أي مساحة.
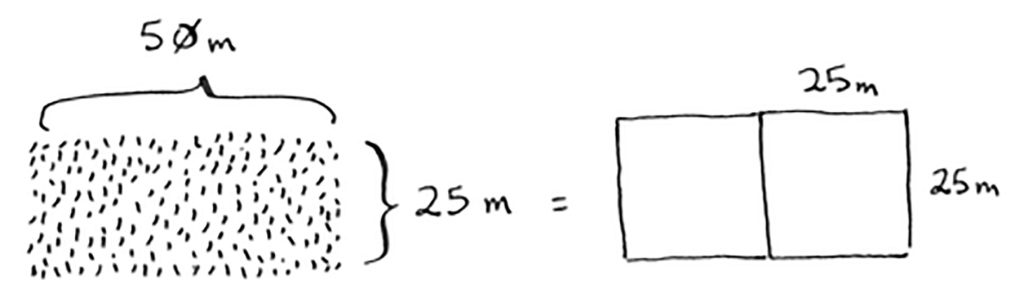
جزء التوقف: عرض الأرض ضعف طولها.
بعد تحديد جزء التوقف سنحدد الجزء العَوْدِي recursive case، وهنا يأتي مفهوم فَرِّق تَسُد. وبحسب هذا المفهوم فإن في كل استدعاء عَوْدِي علينا تصغير (تقسيم) المسألة، أي فَرِّق.
كيف نصغر المسألة في كل مرة؟
حسنًا، سنبدأ الحل. لنعثر أولًا على أكبر مربع في الأرض، بما أن طولها ٦٤٠ مترًا وهو أصغر من عرضها الذي هو ١٦٨٠ مترًا، فإننا سنقسم المزرعة إلى جزء كبير، وهو أكبر جزء، وطوله ٦٤٠ مترًا وعرضه ٦٤٠ مترًا.
وثم سيتبقى لنا من الأرض ١٠٤٠ مترًا، هل المساحة كافية لإنشاء مربع كبير مثل أخيه السابق الذي طوله ٦٤٠ مترًا وعرضه ٦٤٠ مترًا؟
نعم، وفي هذا التقسيم الثاني سيظهر لنا مربعين كبيرين طولهما ٦٤٠ مترًا وعرضهما ٦٤٠ مترًا، وستتبقى مساحة فارغة قدرها ٤٠٠ متر، ٤٠٠×٦٤٠ م.
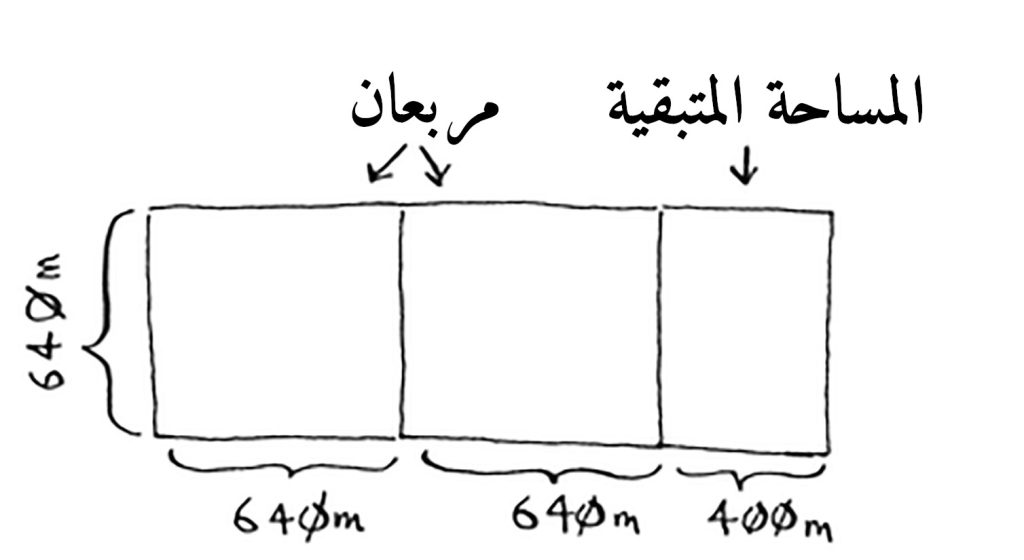
ما رأيك أن نقسم هذه المساحة المتبقية أيضًا بنفس الخوارزمية السابقة التي أنتجت لنا المربعين الكبيرين؟
بما أن العرض لهذه المساحة المتبقية هو ٤٠٠ متر والطول ٦٤٠ مترًا ونحن نريد تقسيمها إلى مربعات متساوية فإننا سنقسم هذه الأرض إلى مربع كبير كما فعلنا في الأولى.
وفي هذه الحالة سيكون عرض المربع الكبير ٤٠٠ متر وطوله ٤٠٠ متر أيضًا، وستبقى لنا قطعة أرض صغيرة قدرها ٢٤٠×٤٠٠ مترًا.
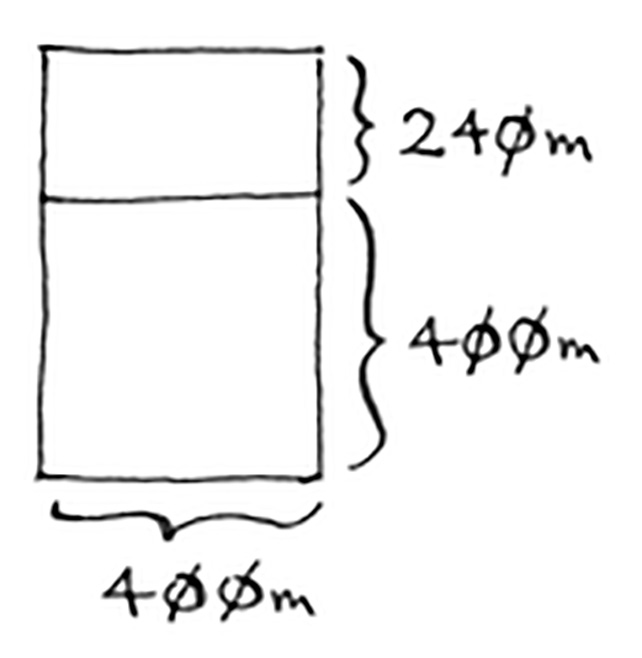
كما ترى، كان حجم مزرعة عبود في البداية ١٦٨٠×٦٤٠ م. وثم أصبح حجم مزرعته أصغر إذ صار حجمها ٦٤٠×٤٠٠ م. وثم صار حجمها الآن ٢٤٠×٤٠٠ م.
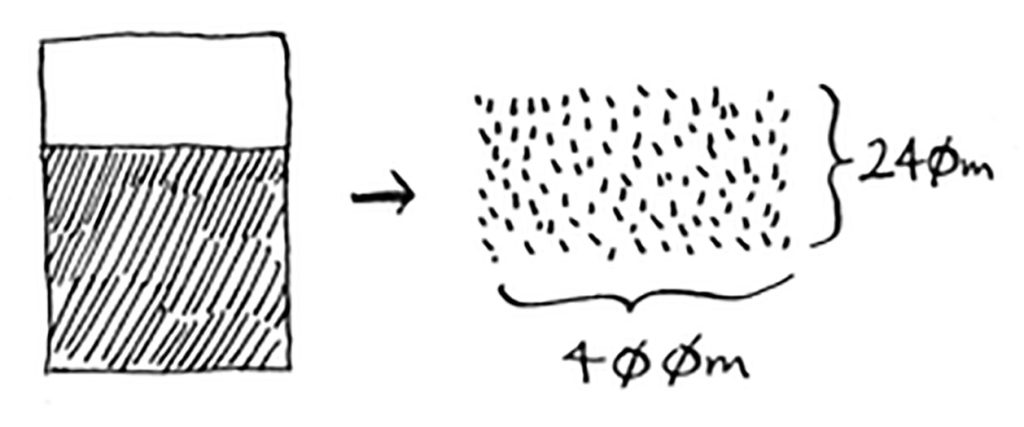
سنقسم هذه الأرض الجديدة التي طولها ٢٤٠ مترًا وعرضها ٤٠٠ متر إلى مربع كبير، وسيكون طول هذا المربع ٢٤٠ مترًا وعرضه ٢٤٠ مترًا أيضًا، وستتبقى لنا مساحة قدرها ١٦٠×٢٤٠ م.
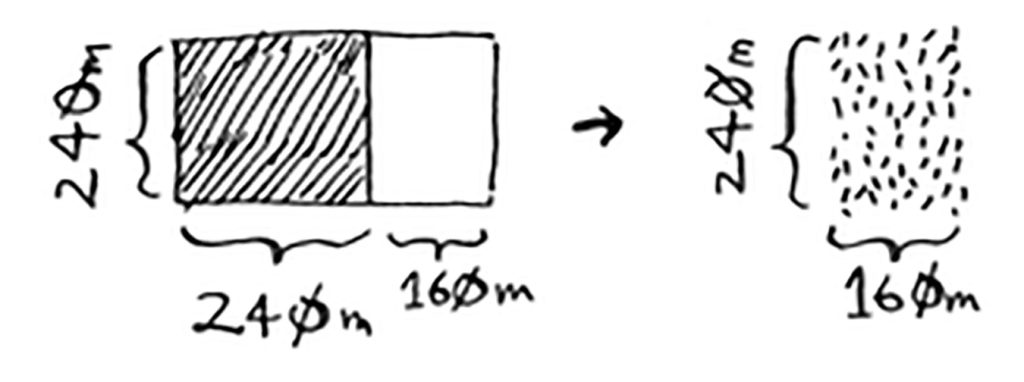
سنعيد الكرة مع قطعة الأرض المتبقية هذه التي عرضها ١٦٠ مترًا وطولها ٢٤٠ مترًا، وسيكون أكبر مربع في هذه الأرض ١٦٠×١٦٠ م. وستكون الأرض المتبقية هاهنا ٨٠×١٦٠ م.
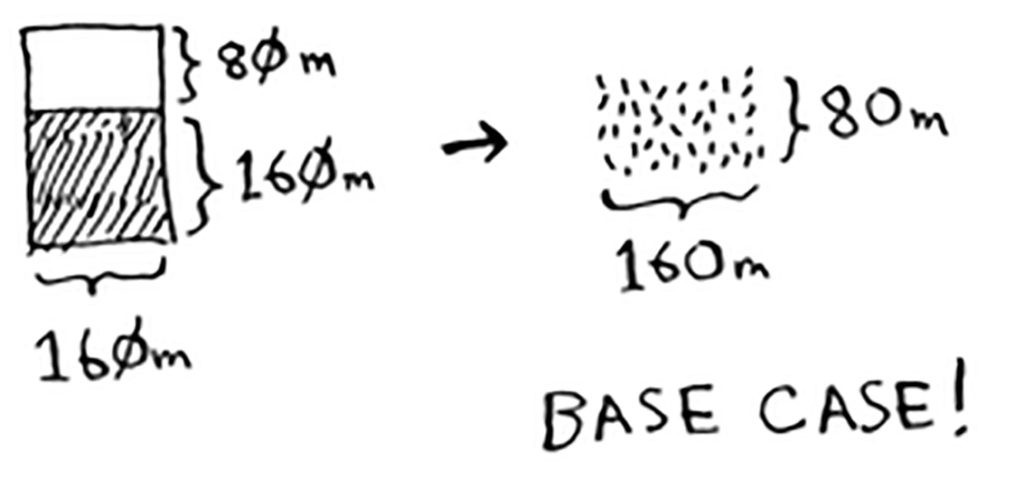
مبارك عليك!
وصلتَ الآن إلى جزء التوقف base case: العرض ضعف الطول، الطول ٨٠ ضعف العرض الذي هو ١٦٠.
الآن نقدر على تقسيم أرض عبود إلى مربعات أصغر طولها ٨٠ مترًا وعرضها ٨٠ مترًا أيضًا، وكل المربعات بأكبر حجم ممكن.
الخلاصة أن سياسة فَرِّق تَسُد:
١. تحدد جزء التوقف
٢. تصغير المسألة لتصل إلى جزء التوقف
سياسة فَرِّق تَسُد ليست خوارزمية لتطبيقها على مسألة، لكنها أسلوب تفكير تفكر به عند حل أي مسألة تواجهك، إذ تفكر حينئذٍ قائلًا: هل أقدر على استعمال سياسة فَرِّق تَسُد لحل هذه المسألة يا ترى؟
تمرين
هل تتذكر خوارزمية البحث الثنائي في الفصل الأول؟
إنها خوارزمية تقوم على مبدأ فَرِّق تَسُد، ولأنها تقوم على هذا المبدأ فالتمرين أن تبين جزء التوقف base case والجزء العَوْدِي لهذه الخوارزمية. فكر!
الخاتمة
ها قد وصلنا إلى نهاية مقالنا المختصر السريع عن مفهوم فَرِّق تَسُد، وفي المقال التالي سنشرح أول خوارزمية فرز تندرج تحت هذا المفهوم، فكن على استعداد وارجع دروسك السابقة!
وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.





