بسم الله الرحمن الرحيم
في عالمٍ لا تسير فيه الأشياء وحدها، بل تتشابك وتتعانق وتتصادم، تبرز نظرية المبيان كعينٍ ثالثة ترى ما لا يُرى، وتسمع همس العلاقات حيث ينعدم الهمس. هذه ليست مجرد فروع وأوراق على شجرة الرياضيات، بل هي جذورها الخفية التي تمتد في كل مجال: من شبكات التواصل إلى أعصاب الدماغ إلى مجرّات الكون.
إنها لغةً تفكّ بها طلاسم الفوضى، وتقرأ بها خريطة الأشياء المتصلة: من أصدقاء في شبكة اجتماعية، إلى أجهزة في شبكة حاسوب، إلى مدن تربطها الطرق. تلك اللغة هي المِبيان!
درس اليوم وما يليه ليسوا كسائر الدروس، وأقول لك: من الآن بدأ الجد الذي لا هزل فيه، وعض على المقالات الآتية بالنواجذ فلها عظيم شأن وأنت لها محتاج أبدًا.
جسور كونيغسبرغ السبعة
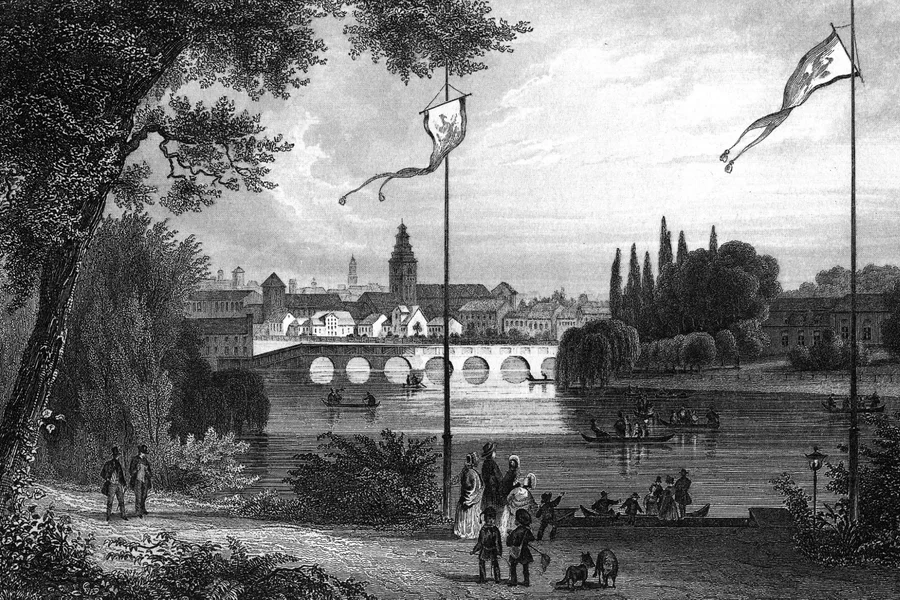
وقف عالم الرياضيات ليونارد أويلر في القرن الثامن الميلادي ( عام ١٧٣٦م) على ضفاف نهر بريجيل في كونيغسبرغ، يتأمل الجسور السبعة التي تربط أجزاء المدينة، إذ خطر له سؤالٌ ظاهره يسير وباطنه عظيم، قلبَ وجهَ الرياضيات، وفتح لها بابًا لم يُطرَق من قبل، وكان السؤال: هل يمكن للمرء أن يسير في المدينة سَيرًا يعبر فيه جسورَها السبعة، كلّ جسرٍ مرةً واحدة لا يكررها، ثم يرجع إلى الموضع الذي ابتدأ منه؟
هذا السؤال، الذي اشتهر في تاريخ الفكر بـ”مسألة جسور كونيغسبرغ السبعة”، لم يكن هزلًا ولا لغزًا يتسلّى به النّاس، بل كان شرارةً أضرمت نار علمٍ جديد، عُرف في ما بعد بـ”نظرية المِبيان”، وذلك بفضل عبقرية الرياضيّ السويسري ليونهارد أويلر، الذي أبصر في المسألة ما لم يُبصره غيره، فصاغ منها أصلًا علميًا، وأرسى بها دعائم فرعٍ من الرياضيات لم يُعرَف من قبل.
جولة في المدينة
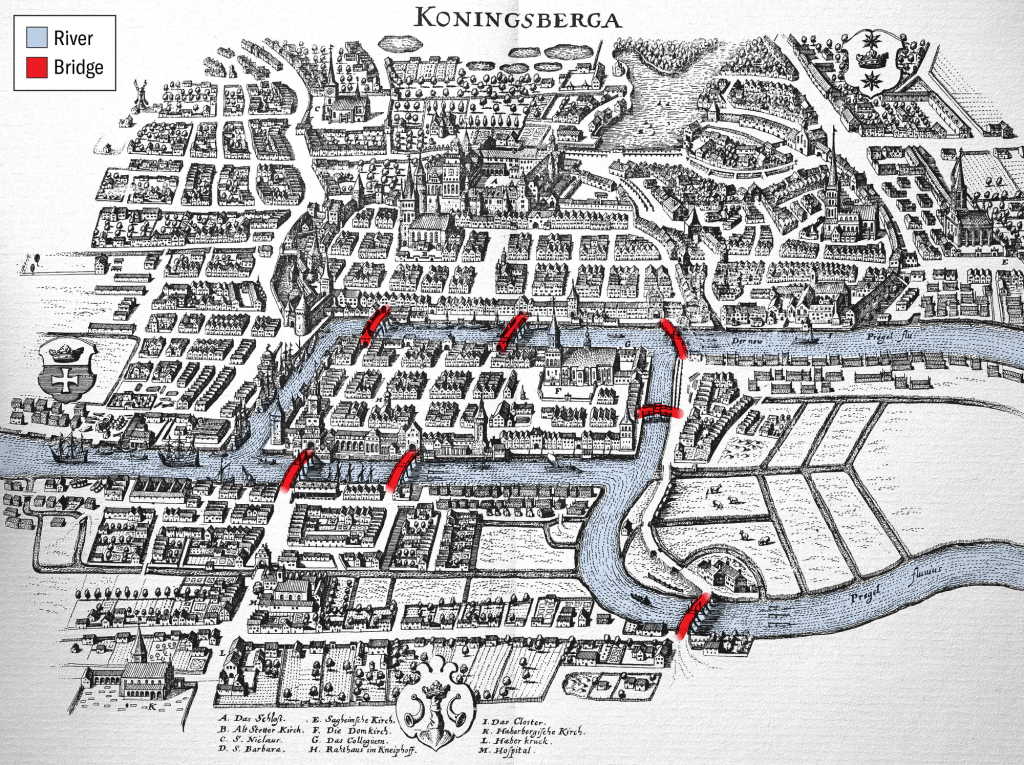
لو كنتَ من سُكّان مدينة كونيغسبرغ، ونظرتَ إلى الخريطة ورأيت جسورها (الصورة في الأعلى)، أكنتَ قادرًا على أن تسلك دربًا تمشي فيه على كل جسر مرةً واحدة لا تزيد ولا تنقص؟ لا جرمَ أنك إن أردتَ الجواب، وجب أن تُعمل الفكر، وتستنير بنور الرياضيات، وتقتفي أثر أرباب النظر الصحيح.
فأول باب يقرعه الناظر في مسائل العدد والمعقول، أن يُغربلَ المعطيات، ويجتثّ الزوائد، حتى لا يبقى إلا صلب المسألة، وهذا هو ما يسميه أهل هذا الشأن “التجريد” (راجع دروس كتاب الساحر). إذ ليست أطوال الجسور، ولا مساحات الأرض، ولا مواضعها من الشمال أو الجنوب مما يدخل في جوهر هذا السؤال.
بل الحق أن الذي يعنينا، هو صلة الأرض بالأرض، وعدد ما يصل بينها من جسور. ومن هاهنا، وجب أن ننبذ الخريطة المعهودة، ونُنشئ مكانها رسمًا لا يظهر فيه إلا دوائر تمثّل اليابسة، وخطوط ترمز إلى الجسور، فيكون الرسم تجريدًا لما هو مهم، وطرحًا لما عداه، هكذا:
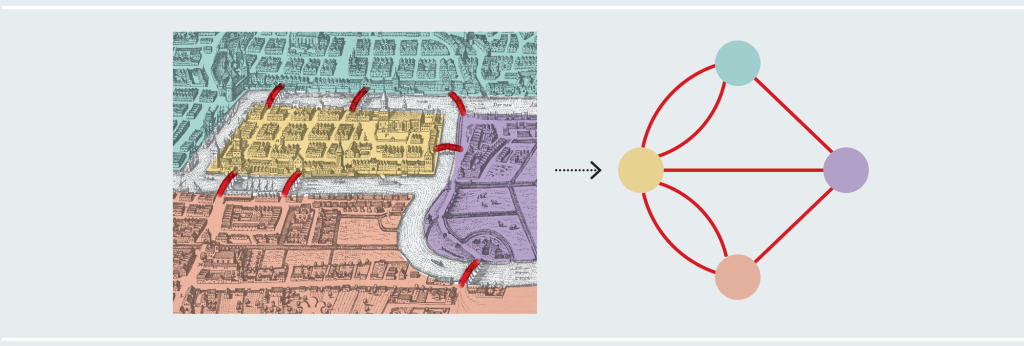
فهذا هو مسلك الرياضيين، وأسلوبهم في النظر: أن يرفعوا عن أعينهم غشاوة الزينة، ويطلبوا جوهر الشيء بما هو هو، لا بما يبدو عليه.
بعد إعمال فكرٍ ليجيب على السؤال سَطّر هذا الرياضيّ السويسريّ النابغة، ليونهارد أويلر، ما توصّل إليه من حل في مقالته الشهيرة الموسومة بـ «حلّ مسألة تتعلّق بهندسة المواضع» (Solutio problematis ad geometriam situs pertinentis)، وهي ورقة علميّة صارت بمنزلة الأساس الذي بُني عليه صرح نظرية المِبيان (Graph Theory)، بل وكانت من أولى اللبنات أيضًا في علم يُعرف اليوم بهندسة المواضع topology. كان جواب السؤال: إنّ ذلك غيرُ ممكن، ولا يكون البتّة، ما لم تتوافر شروطٌ مخصوصة!
ثمّ لم يكتفِ بالجواب، بل رفع المسألة من حيّزها الخاص إلى قاعدةٍ عامّة، فاختزل معالم المدينة إلى نقاطٍ تمثّل الضفاف، وخطوطٍ تمثّل الجسور، وبذلك كانت أوّل نواةٍ في نظرية المِبيان.
قد تضمن هذا العمل الجليل، أقصد ورقته البحثية، على فكرتين عظيمتين كان لهما أبلغ الأثر في تطور الفكر الرياضي:
- التجريد (Abstraction): أن تُختزل المسائل الواقعية، مهما بدا ظاهرها معقدًا، إلى عناصر: عقد تمثل الكيانات، وروابط تربط بين العقد، وهي قد تمثل العلاقات أو الروابط. وهكذا يُنظر إلى “ما هو” لا “ما يبدو”.
- التعميم (Generalization): أن يُستخرج من المسألة الخاصّة قاعدة تنطبق على جميع المسائل المماثلة، لا على كونيغسبرغ وحدها، بل على كل مِبيان graph مهما كانت طبيعته أو تعقيده.
ومن هذا النظر الدقيق خرج بـنظريةٍ سُمّيت باسمه وكانت ثورة في الفكر الرياضي، إذ نقلت الرياضيات من العالم الماديّ إلى عالم العلاقات والصيغ، ومهّدت السبيل لعلوم الحاسوب والشبكات والمنطق الحديث.
نظرية المِبيان
نظريةالمِبيان (بكسر الميم) فرعٌ من فروع الرياضيات المنفصلة Discrete Mathematics، تختص بدراسة خصائص وتطبيقات المِبيان graph، بها تُدرَس الروابط بين الكيانات أكانت أشخاصًا أم مدنًا أم عقدًا في شبكة أم سائر ما يتشابك ويتّصل، فكلما كان ثمّة أشياء مترابطة، أفرادًا أو مدنًا أو عقدًا في شبكةٍ أو ذرات في مركّب، فإنّ نظرية المِبيان هي لسان حال تلك الروابط، وصورة تمثّل جوهرها.
فهذه النظرية وإن نشأت من مسألةٍ في الجسور، فقد امتدت حتى شملت شبكات التواصل الاجتماعي إلى أنظمة النقل، ومن الدوائر البرقية Electrical circuits إلى الخرائط، بل كل ما في الوجود من روابطٍ تُدرَك بالعقل وإن خفيت على الحسّ.
المبيان graph: نسيجٌ من العُقَد nodes والوُصَل Edges، حيث تمثل العُقَد مواضع أو كيانات، وتمثل الوُصَل ما بينها من علائق وروابط (وللوُصَل اسم آخر غير العُقَد، اسمها في الرياضيات هو Vertices). انظر الصورة:
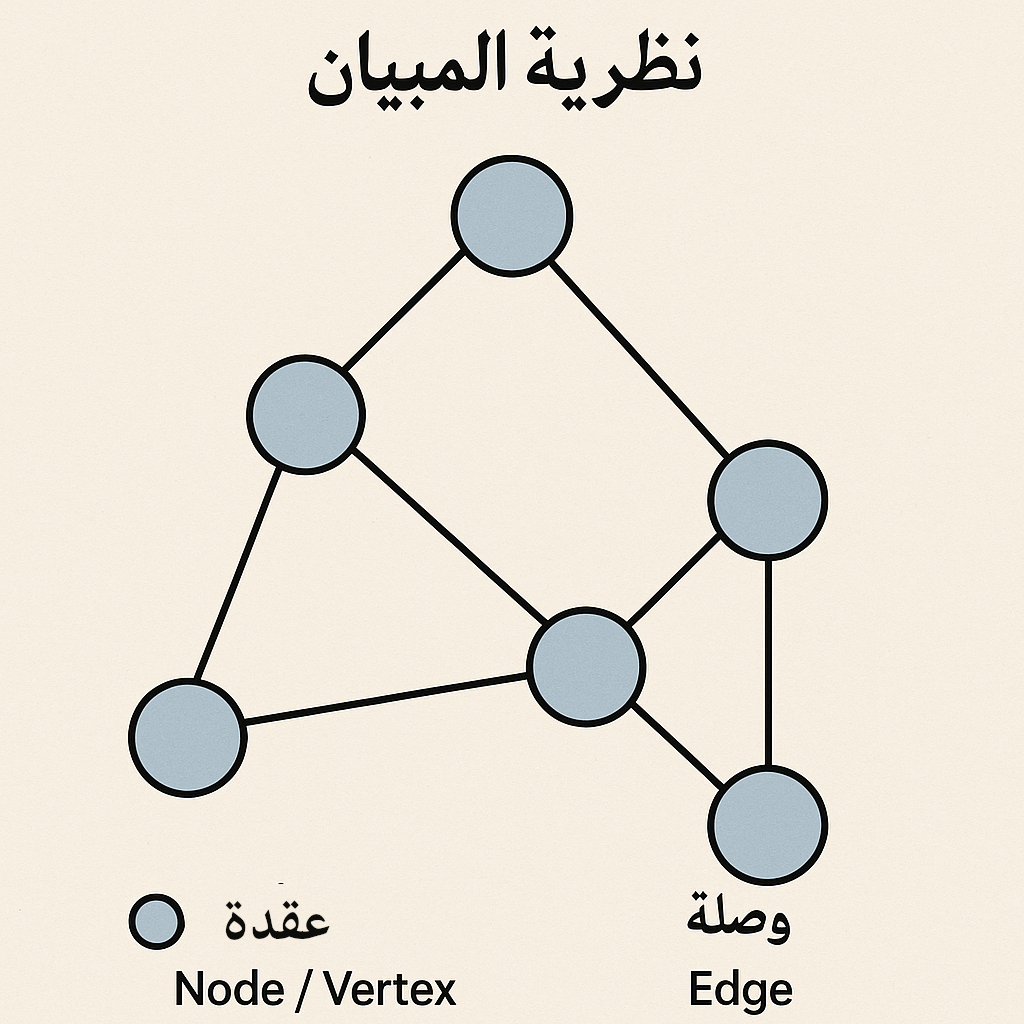
وتفصيله:
- العُقَد node: هي نقاطٌ أو مواضع في المبيان، كالمدن في خريطة الطرق
- الوُصَل edge: هي الروابط بين العُقَد، كالطرق بين المدن (كل خط هو وصلة، أما الدوائر فهي العُقَد التي تربط بينها الوصلة)
أصناف المبيانات
المِبيان أصناف، واعلم أن نظرية المِبيان لا يتسع لها مقال واحد، بل كتاب كامل، وإنما أنا أذكر ما يُسهِّل لك فهم الدرس والتعلم من الكتاب، وأصنافه:
المبيان المُطلَق Undirected Graph: مبيانٌ لا اتجاه لوُصلاته، فكل وُصلةٍ تسري في كلا الوجهين، كالطريق المسلوك ذهاباً وإياباً.
المبيان المُوجَّه Directed Graph (Digraph): مبيانٌ ذو وُصلاتٍ مُوجَّهة، كالسهم له رأسٌ ومَقصِد
المبيان المَوزون Weighted Graph: مبيانٌ لكل وُصلةٍ فيه ثِقلٌ أو قيمة
المبيان المُتَّصِل Connected Graph: مبيانٌ يُفضي فيه مَسلكٌ من كل مَنقطٍ إلى كل مَنقطٍ آخر
المبيان المُنقَطِع Disconnected Graph: مبيانٌ لا تتصل فيه جميع المناقط بمسالك
المبيان الدَّوَّار Cyclic Graph: مبيانٌ فيه دَورٌة واحدة على الأقل
المبيان لا دَوري cyclic Graph: مبيانٌ خالٍ من الدورات
ولنضرب أمثلةً لإيضاح هذه الأصناف:
تأمل جماعةً من الأصحاب كمبيانٍ مُطلَق، حيث الوُصلة بين صاحبين تعني معرفة كلٍ منهما بالآخر. فإذا عرف سعدٌ خالداً، فخالدٌ يعرف سعداً بالضرورة.
أما في المبيان المُوجَّه، فتأمل أهل المِنصَّة (تويتر). فالوُصلة من سعدٍ إلى خالدٍ تعني أن سعداً يتابع خالداً، ولا يلزم أن يكون خالدٌ متابعاً لسعد.
وفي المبيان المَوزون، تأمل البلدان والطرق بينها. فالمناقط هي البلدان، والوُصلات هي الطرق، وثِقل كل وُصلةٍ هو المسافة بين البلدين.
والمبيان المُتَّصِل كجماعةٍ يعرف كل فردٍ فيها الآخرين جميعاً. أما المبيان المُنقَطِع فكجماعةٍ لا يعرف بعض أفرادها بعضاً.
الخاتمة
ها قد وصلنا إلى نهاية المقال، وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.