كتاب استيعاب الخوارزميات، الفصل السادس، خوارزمية البحث المتسع Breadth-First Search
بسم الله الرحمن الرحيم
 حان وقت دراسة المِبيان تطبيقيًا وتعلم أول خوارزمية لذلك
حان وقت دراسة المِبيان تطبيقيًا وتعلم أول خوارزمية لذلك
وهي خوارزمية البحث المتسع breadth-first search algorithm، اختصارًا BFS، فالخوارزمية تظهر لك أقصر طريق بين شيئين، وقد يكونان أشياء كثيرة، فمن فوائد الخوازمية أنك قد تكتب:
حاسب يحسب لك أقل الخطوات للفوز في لعبة.
مدقق إملائي!.
العثور على أقرب مبرمج أو مقوت في حارتك أو سوق قات.
الوصول للصوص أو تتبع مشتبه به أو إيجاد قسم شرطة.
بأسرع الطرق والكثير الكثير الكثير من الفوائد الاخرى.
 أهمية خوارزمية المِبيان
أهمية خوارزمية المِبيان
خوارزمية المِبيان من الخوارزميات النافعة لكثرة ما ستستعلمها في عملك إن شاء الله، فتابع المقالات التالية فإن لها عظيم شأن يا مبعسسنا الكريم.
 دروس سابقة لفهم درس اليوم
دروس سابقة لفهم درس اليوم
حتى تفهم درس اليوم لا تنس الدروس السابقة في هذا الفصل، وهي دروس الصف ومقدمة لنظرية المِبيان:
 الشيخ عبود وأقصر طريق
الشيخ عبود وأقصر طريق
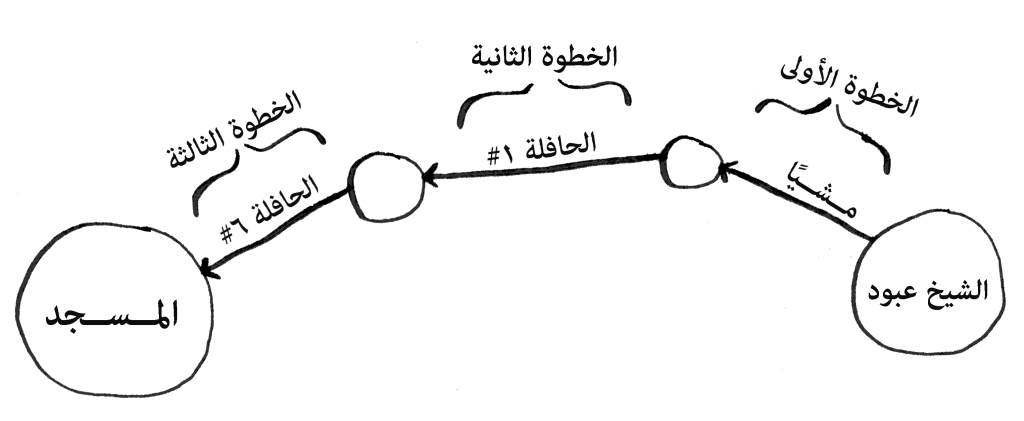
سافر الشيخ عبود إلى مدينة قاصدًا هداية الناس داعيًا إلى الحق، وعند وصوله كان يبحث عن مسجد للصلاة. ولشدة تعبه من السفر أراد الوصول إلى المسجد بأقصر طريق، فهو كهل والشيب قد غزا مفرقاه.
- سأل أحدهم عن أقرب مسجد وقد دله عليه وأعطاه خريطة، نظر إلى الخريطة؟ وعرّعرّ! لأنه من الجيل القديم.
- وكان عليه السير إلى أقرب محطة للحافلات، وكل محطة توصل إلى ما تليها.
- لم يجد حافلة توصله إلى وجهته رأسًا، بل عليه أن يستقل حافلة من مكان إلى مكان.
 ترتيب الحافلات للوصول إلى المسجد
ترتيب الحافلات للوصول إلى المسجد
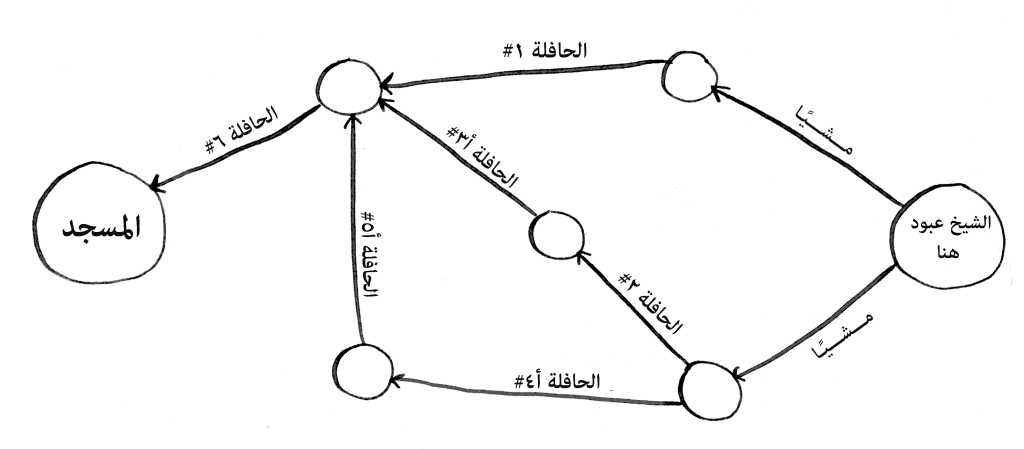
- مشيًا إلى أقرب محطة حافلات، وهي الحافلة #١ والحافلة #٢.
- ثم يستقل واحدة إلى المحطة التالية.
فهلّا: أعنت الشيخ ودللته على أقصر طريق للوصول إلى المسجد؟ ما أقل خطوات يفعلها الشيخ للوصول إلى المسجد؟
هيا نعين الشيخ عبود ولنا الأجر. وقبل أن أخبرك بالحل انقلها إلى ورقة وقلم وجرب حلها ثم اجعلها خوارزمية بلغة البرمجة التي تجيدها! هذا تحدٍّ لك، فهل أنت له؟!
لا تختلس النظر وجرب حلها ثم فلتأتِ لرؤية الحل.
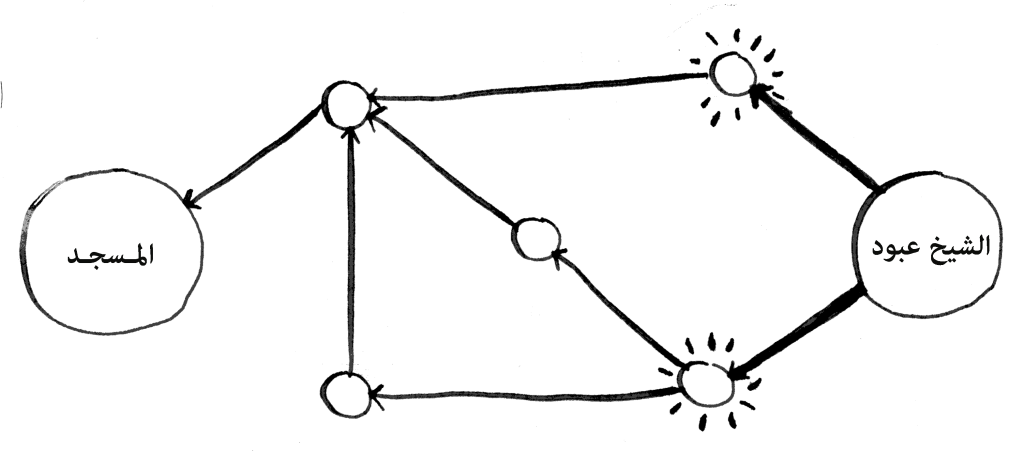
 سأسأل سؤالًا لحلها: هل يستطيع الشيخ العبود العبور في خطوة واحدة؟
سأسأل سؤالًا لحلها: هل يستطيع الشيخ العبود العبور في خطوة واحدة؟
نجرب:




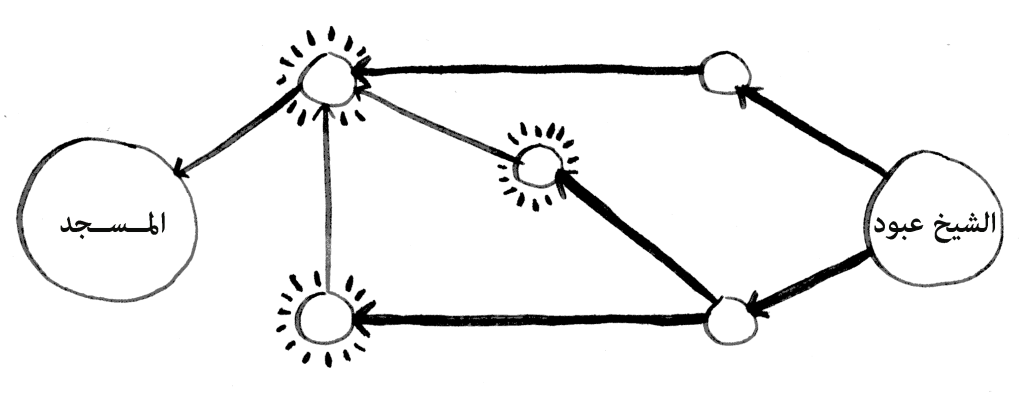
أيستطيع العبور في خطوتين؟



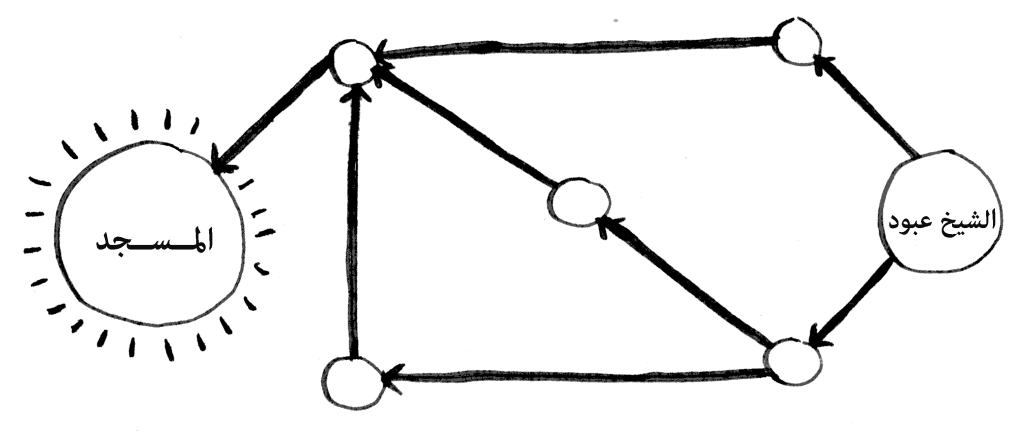






 ما نوع هذه المسائل؟
ما نوع هذه المسائل؟

shortest-path problem

-
أقصر طريق إلى بيت صاحبك او حبيبتك
-
أقل عدد من الخطوات للفوز في الشطرنج
-
أو أي هدف يتطلب الوصول بأقل تكلفة أو وقت
 ما الخوارزمية المناسبة لهذا النوع؟
ما الخوارزمية المناسبة لهذا النوع؟

خوارزمية البحث المتسع
Breadth-First Search (BFS)
وأحب تسميتها:
خوارزمية البحث المُسَعرِض 
 خلاصة الفِقرة:
خلاصة الفِقرة:

-
حللنا المسألة هذه بتمثيلها في مِبيان (graph)
-
ثم طبّقنا خوارزمية البحث المتسع (BFS) عليها


📊 المِبيان Graph
المِبيان graph هو نسيجٌ من:
-
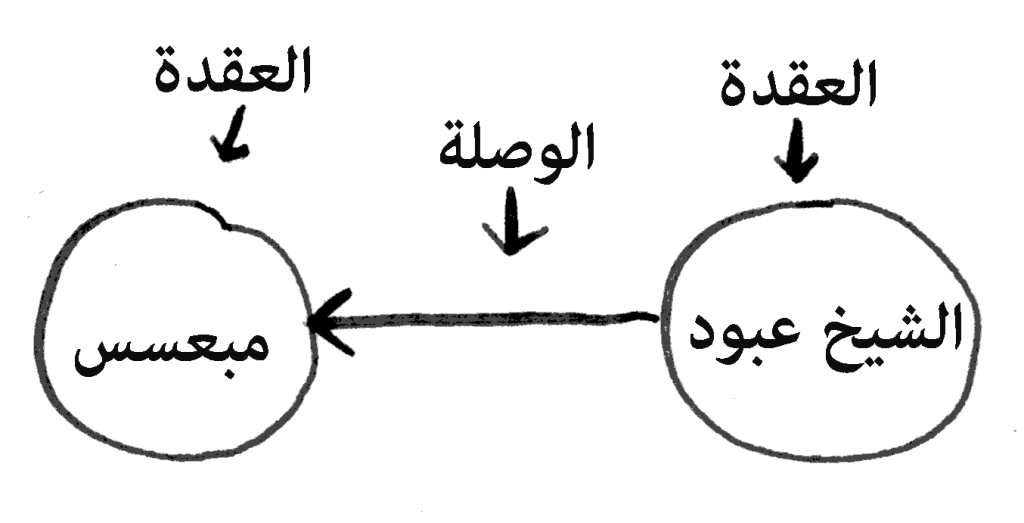
العُقَد (nodes) والوُصَل (Edges)
حيث تمثل العُقَد مواضع أو كيانات، وتمثل الوُصَل ما بينها من علائق وروابط.
📍 العُقَد (node):
نقاطٌ أو مواضع في المِبيان، مثل:
-
المدن في خريطة الطرق ومحطات الحافلات 🚏
🔗 الوُصَل (edge):
هي الروابط بين العُقَد، مثل:
-
الطرق بين المدن
-
كل خط هو وصلة
-
أما الدوائر فهي العُقَد التي تربط بينها الوصلة
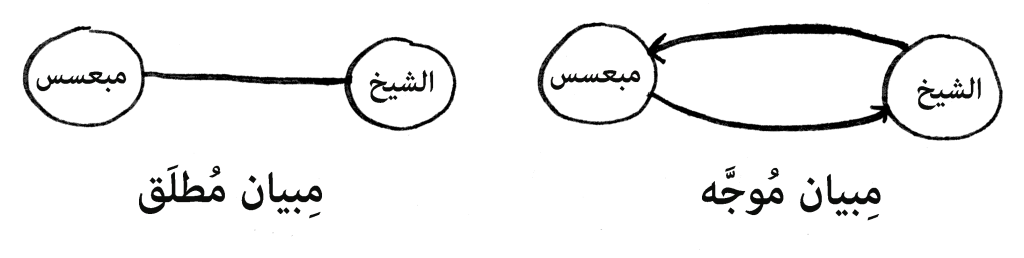
✏️ سأمثل لك علاقة الشيخ عبود مع صاحبه مبعسس في مِبيان، انظر:
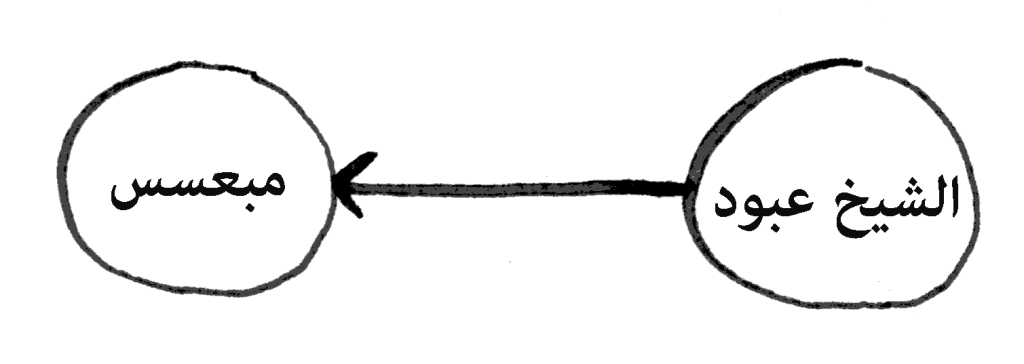
وهذا تمثيل للشيخ عبود وأصحابه:
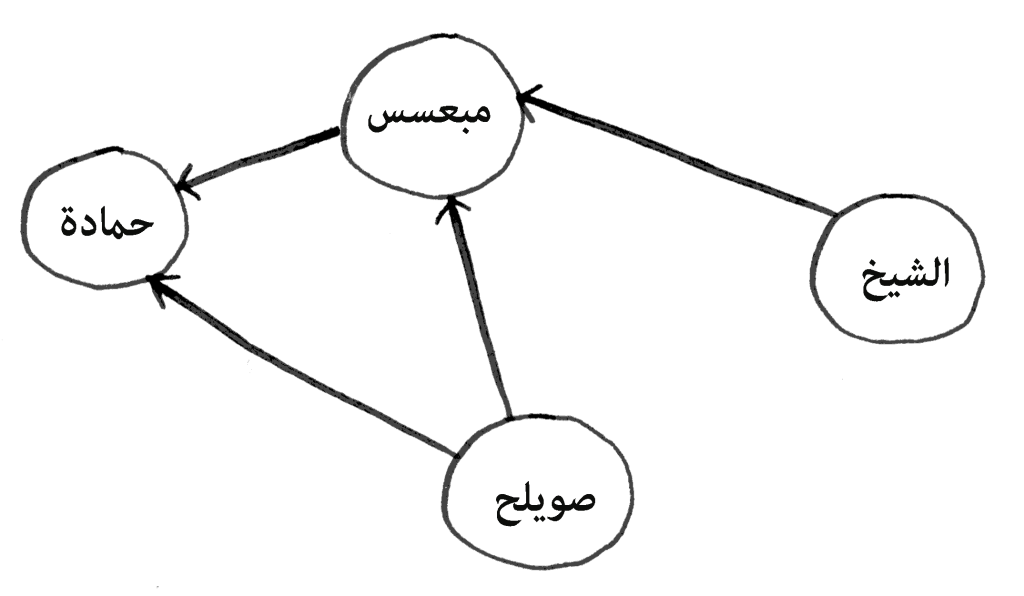
🔗 المِبيان ليس إلا العُقَد والوصلات،
حيث تُعبّر الوصلة (edge) عن الرابط بين العُقَد (nodes).
✏️ فالوصلة هي الخط الواصل بين عقدتين.
🏘️ مفهوم الجار في المِبيان
-
العقدة التي تتصل بغيرها رأسًا، أي بينها وبين عقدة أخرى وصلة، تكون جارًا لها.
-
مثال:
-
الشيخ عبود جار مبعسس ✅
-
لكن حمادة ليس جار الشيخ عبود ❌، لأنّه لا وصلة تصل الشيخ بحمادة مباشرة، ولا وصلة تخرج من عقدة الشيخ إلى عقدة حمادة.
-
-
وصويلح جار مبعسس وجار حمادة، لأن بينهم وبين صويلح وصلة، وصلة تخرج من عقدة صويلح إلى عقدة مبعسس وحمادة وتتصل بهما رأسًا.
⚠️ لا تنس جزيئة الجار هذه! وهيا بنا إلى نوعي المِبيان نحتاجهما في درس اليوم، وهما المِبيان الموجَّه والمِبيان المُطلق.
المِبيان الموجَّه والمُطلَق
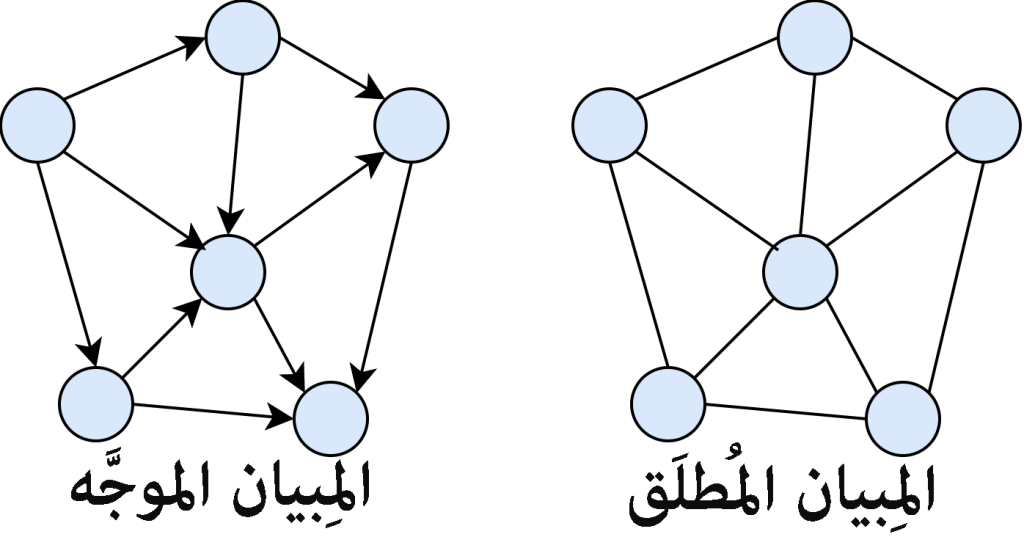
قلت في المقال السابق عنهما:
-
المبيان المُطلَق (Undirected Graph):
مبيانٌ لا اتجاه لوُصلاته، فكل وُصلةٍ تسري في كلا الوجهين، كالطريق المسلوك ذهاباً وإياباً. -
المبيان المُوجَّه (Directed Graph أو Digraph):
مبيانٌ ذو وُصلاتٍ مُوجَّهة، كالسهم له رأسٌ ومَقصِد.
وانظر في الصورة:
-
في المِبيان المُطلَق ليس للوصل فيه سهم يوجه اتجاهها، فالوصلة تسير في الاتجاهين.
مثال: السهم يخرج من عقدة الشيخ عبود إلى عقدة مُبعسس (تخيل معي المِبيان)، ثم السهم يعود من عقدة مبعسس إلى عقدة الشيخ عبود.
باختصار الوصلة تسير في اتجاهين، لذلك لا نرسم لها سهمًا، لأن علاقتها ثنائية الاتجاه. -
أما في المِبيان الموجَّه، فالسهم يدل على اتجاهه “اتجاه الوصلة”.
مثال: السهم يخرج من عقدة الشيخ عبود إلى عقدة مبعسس فحسب. ولا يعود أدراجه.
للوصول من مبعسس إلى الشيخ عبود يجب البحث عن طريق آخر لذلك.
إذًا باختصار الوصلة تسير في اتجاه، علاقتها وحيدة الاتجاه.
أمثلة:
-
في مواقع التواصل، مثل فيسبُك Facebook:
-
إذا كنت تتابع صديقًا وهو يتابعك، فهذا مِبيان مُطلَق (علاقة متبادلة).
-
إذا كنت تتابعه وهو لا يتابعك، فهذا مِبيان موجَّه.
-
نصيحة للمبعسس الذي يقرأ المقالة:
إن كنت تصبو لأن يكون لك شأن في الاختصاص وينفعك العلم ويؤتي ثمرته، فقف هاهنا، تفكَّر، واعمل عقلك في الفكرة، وتفكّر في اقتراحات الصداقات؟ وفي الخرائط؟ وفي كل ما حولك!ولا تنس قول الشيخ الجيل محمد أبو موسى أطال الله عمره:
“أَثْقِلْ الفِكرَةَ في نَفسِك، واسقِها من فَهمِك وتدبّرك، ولا تُخرِجْهَا إلا وهي تَحمِل شيْئًا من عَبَقِ نَفسِك!”
📊 الصورة التالية كليها متساويان، فهما مِبيان مُطلَق، فانظر وتفكَّر:
🔍 خوارزمية البحث المتسع (BFS)
خوارزمية البحث المتسع تختلف عن الخوارزميات التي درسناها في الفصول السابقة، إذ إنها تُطبّق على المِبيان (Graph)، وتُجيب على نوعين من الأسئلة:
❓ ما نوع الأسئلة التي تجيب عليها BFS؟
-
🛣️ ما أقصر طريق من العقدة س إلى العقدة ص؟
-
🔗 أمن طريق من العقدة س إلى العقدة ص؟
🧭 مثال توضيحي للنوعين:
النوع الأول، أقصر طريق، قد رأيناه ونحن نساعد الشيخ عبود في الوصول إلى المسجد، لكن ما النوع الثاني؟ ما المقصود به؟
والثاني: هب أنك مزارع 👨🌾، “مزارع بُن وليس قات” وثمرك في إبانها قد نضج 🍇، وقد آن قطافه، وتريد بيعه.
فتبدأ البحث عن مشتري، مثلًا عبر منصة الفيسبُك بين أصدقائك 👥.
-
إن وجدت مشتريًا بين أصدقائك ✅ → توقفت عن البحث، وبِعت له.
-
إن لم تجد ❌ → تبحث بين أصدقاء أصدقائك، وهكذا تتوسع دائرة البحث تدريجيًا.
🌀 هذا هو جوهر خوارزمية البحث المتسع:
تبدأ من الدائرة الأقرب، ثم تنتقل إلى الأبعد طبقةً طبقة.

👥 كيف تعمل خوارزمية البحث المتسع عمليًا؟
تأتي بالأصدقاء كلهم في لائحة 📄 وتبدأ البحث فيهم:
“من يشتري ثمري؟ 🍇”
-
إن عثرت على مشترٍ ✅ → تتوقف عن البحث وتبيع له.
-
إن لم تجد أحدًا ❌ → تواصل البحث في نطاق أوسع.
🧠 التوسّع إلى طبقات:
إذا لم تجد المشتري في أصدقائك المباشرين،
👥 فعليك أن تبحث في أصدقاء أصدقائك، نصنف اللائحة إلى طبقات:
-
طبقة أولى: أصدقاؤك
-
طبقة ثانية: أصدقاء أصدقائك
-
طبقة ثالثة: أصدقاء أصدقاء أصدقائك
-
وهكذا…
📌 تخيّل:
🔵 دائرة تحتوي على أسمائك أصدقائك
🟢 ثم دائرة أكبر تحتوي على أصدقاء أصدقائك
🟣 ثم ثالثة أكبر لأصدقاء أصدقاء أصدقائك، ونصيحتي لك أن تستهدف المزز بالعاطفة فهي أسهل الطرق للبيع.
🌊 لماذا تُسمّى “البحث المتسع”؟
لأن الخوارزمية:
-
تتوسع طبقةً طبقة
-
تستعرض كل طبقة بالكامل قبل أن تنتقل لما يليها
🧭 ولذلك أُحب أن أسميها:
خوارزمية البحث المستعرض
🤔 سيسألني المبعسس الذكي الآن ويقول:
“كيف نضمن أننا لا نبحث في الطبقة الثانية أو الثالثة فتختلط الطبقات قبل إنهاء الأولى؟”
🔑 والجواب:
في مقال الصف (Queue). لم نتعلّم الصف عبثًا!
بل هو الأساس الذي يُنظّم طريقة البحث، وبه نضمن عدم اختلاط الطبقات، فأنا أوطئ لك بمقالات حتى تفهم القادم،
هيا بنا إلى التطبيق العملي! 💻
سنبرمج المِبيان في بايثون 🐍 ثم نُطبّق عليه خوارزمية البحث المتسع!
💻 برمجة المِبيان (Graph)
🤔 كيف سنبرمجه؟
عليك أن تفكر وتحاول أيها الـمُبعسس القادم، فهذا من صُلب البعسسة!
فإن لم تُجرب وتحاول وتنظر في حلك، فكبِّر على عقلك ثلاثًا فقد عطلته 🧠🔕🔕🔕
⚠️ إياك أن تخشى الفشل!
💡 مهما كان عدد الأخطاء، فهي بداية الطريق نحو النجاح.
🧱 الأخطاء ليست نهاية، بل أهم لبنة في بنائك وتعلّمك.
🚫 لكن لا تيأس، فكل من نجح كان في البداية مُخفقًا.✊ استمر… تعلّم… وامضِ قُدمًا! وتابعني ❤️ واعمل إعجاب ومشاركة 🙏 ولا تنسَ الدعاء !
📚 استرجاع سريع:
تعلمنا الكثير حتى الآن وبما تعلمناه سنبرمج به المِبيان. قلنا المِبيان:
المِبيان = عقد (Nodes) + وُصل (Edges)
وكل عقدة قد تتصل بجارتها 👥
🔄 تمثيل العلاقة برمجيًا
إذا سألتك:
“كيف تمثل العلاقة بينك وبين صاحبك برمجيًا في بايثون أو أي لغة أخرى تتقنها فما جوابك؟”
أنا أفكر، أحلل سؤالك:
-
العلاقة = شيء يربط بين كيانين بين هذا وذاك ويتعلق به؟
-
ما الذي يمكنني من ربط شيء بشيء مما درسته عند مبعسس؟
🧠 نعم أسمعك أيها المبعسس العظيم، فإن أجبت بقولك: جدول التلبيد Hash Table
👏 فإني أحييك! أحسنت أحسنت أيها المبعسس الذكي!
🧩 لماذا جدول التلبيد (Hash Table)؟
لأنه:
-
يقرن مفتاحًا بقيمة
-
ونحن نريد ربط العقدة بـ جيرانها
✨ الله أكبر فُرجت بحمد الله!
🐍 في لغة بايثون نكتب التالي لإنشاء جدول تلبيد:
graph = {}ثم ننشئ عقدة، والتي هي مفتاح، ثم ونسند لها القيم التي نريد، وهي في حالنا سائر العقد المتصلة بالعقدة:
graph[“you”] = [“allunlocker.com”, “Muhammed”, “Ahmed”]العقدة you والتي تعني أنت، مقترنة بصفيفة Array فيها كل جيران عقدتك.
إن أردت مِبيانًا مثل ذاك الذي كان فيه الشيخ عبود ومبعسس وصويلح وحمادة، والعلاقة بينها متشابكة فأمره سهل، انظر:
graph["aboud"] = ["bassye.org"]
graph["bassye.org"] = ["hamada"]
graph["sweileh"] = ["bassye.org", "hamada"]❓ سؤال لك:
إذا أضفنا صويلح قبل حمادة، فهل هذا يضر؟
أله ضرر أو تأثير؟
🧠 الجواب: إن عدت إلى درس جدول التلبيد (Hash Table)، فستجد أنه لا يعبأ بالترتيب.
🔁 الترتيب لا يؤثر على النتيجة، لذا لا تقلق بشأن من يسبق من.
📚 راجع الدروس للمزيد من الفهم…
🧮 برمجة خوارزمية البحث المُتسِع (BFS)
🚀 هيا نبرمج الخوارزمية التي سنطبقها على المِبيان: خوارزمية البحث المُتسِع
🧾 حان أوان الإتيان بالصف Queue، فنحن نحتاجه الآن.
سنبرمجها بهذا الشكل، أي تنفيذها (Implementation) سيكون كما يلي:
بداية سننشئ صفًّا مزدوج النهاية double-ended queue، وهي في بايثون deque:
from collections import deque
search_queue = deque()
search_queue += graph[“you”]تذكر أن graph[“you”] سيُرجع كل العقد المتصلة بعقدتك، وكلها ستُضاف إلى متغير search_queue:
while search_queue:
person = search_queue.popleft()
if person_is_buyer(person):
print person + “ is the buyer!”
return True
else:
search_queue += graph[person]
return Falseتحتاج الآن إلى الوظيفة person_is_buyder، التي تخبرك أهو المشتري أم لا؟
def person_is_buyer(name):
return name[-1] == ‘b’الوظيفة تفحص آخر الاسم هل انتهى بالحرف B، والذي يرمز للمشتري، أم لا، لغرض الشرح فحسب وليس بالجد.
انظر كيف ستعمل الخوارزمية خطوة بخطوة:

🔄 تستمر الخوارزمية في العمل حتى:
-
✅ تجد المشتري
-
🈳 أو يصير الصف فارغًا وخاليًا
⚠️ لكن… في الرماز السابق عِلّة!
🧩 إذ ستعمل الخوارزمية في حلقة لا انتهاء لها (infinite loop)، وتبقى تبحث عن المشتري حتى تجده، دون مراعاة تكرار الأشخاص الذين تم البحث فيهم مسبقًا.
📜 الآن، سأعطيك الرماز كاملًا.
🧠 مهمتك: دراسته وتحديد العِلّة التي قمنا بحلّها:
from collections import deque
def person_is_buyer(name):
return name[-1] == 'm'
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["bob"] = ["anuj", "peggy"]
graph["alice"] = ["peggy"]
graph["claire"] = ["thom", "jonny"]
graph["anuj"] = []
graph["peggy"] = []
graph["thom"] = []
graph["jonny"] = []
def search(name):
search_queue = deque()
search_queue += [name]
# This is how you keep track of which people you've searched before.
searched = set()
while search_queue:
person = search_queue.popleft()
# Only search this person if you haven't already searched them.
if person in searched:
continue
if person_is_buyer(person):
print(person + " is the buyer!")
return True
search_queue += graph[person]
# Marks this person as searched
searched.add(person)
return False
search("you")🧮 تعقيد الوقت لخوارزمية البحث المتسع (BFS)
إذا كنت ستبحث في كل معارفك (أي في شبكة المعارف الكاملة) عن المشتري:
-
🔗 فأنت ستتبع كل وصلة.
-
الوصلة قد تكون:
-
➡️ سهمًا يشير إلى شخص في شبكة المعارف.
-
🧭 أو طريقًا “وصلة” يربط بينك وبين غيرك، هذه واحدة.
-
🧱 خطوات التنفيذ:
-
👥 يتم إضافة شخص واحد إلى الصف (Queue) في كل مرة.
-
⏱️ تعقيد الوقت لإضافة شخص إلى الصف هو:
O(1) -
🔁 عند تكرار هذا لجميع الأشخاص يعطي تعقيد وقت قدره:
O(V)حيث V هو عدد الأشخاص.
✅ إذن تعقيد الوقت لخوارزمية البحث المتسع سيكون:
(عدد الأشخاص + عدد الوُصَل)O، والمشتهر كتابتها هكذا:
O(V+E)فالحرف V يرمز إلى الوُصل، أما الحرف E فيرمز إلى العقد، واضحة!
🔸 حيث:
-
V= عدد الوُصَل (Edges) 👉 أي الأشخاص أو الكيانات -
E= عدد العُقَد (Nodes) 👉 أي العلاقات أو الروابط
🔹 واضحة!
 ختامًا لا تنسونا من دعائكم
ختامًا لا تنسونا من دعائكم 
ها قد وصلنا إلى نهاية المقال، وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو أنني قد وفّقت في الشرح.
وفي نهاية الأمر، لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطئ، فإن وفقت في طرح الموضوع فمن اللّٰه عز وجل، وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع.
لا تنسوا الدعاء لكل من ساهم في “عجن وخبز” هذه المقالة،
ولا تنسوا إخوانكم في فلسطين 
والسلام عليكم ورحمة اللّٰه تعالى وبركاته.

 درس الصف
درس الصف 





