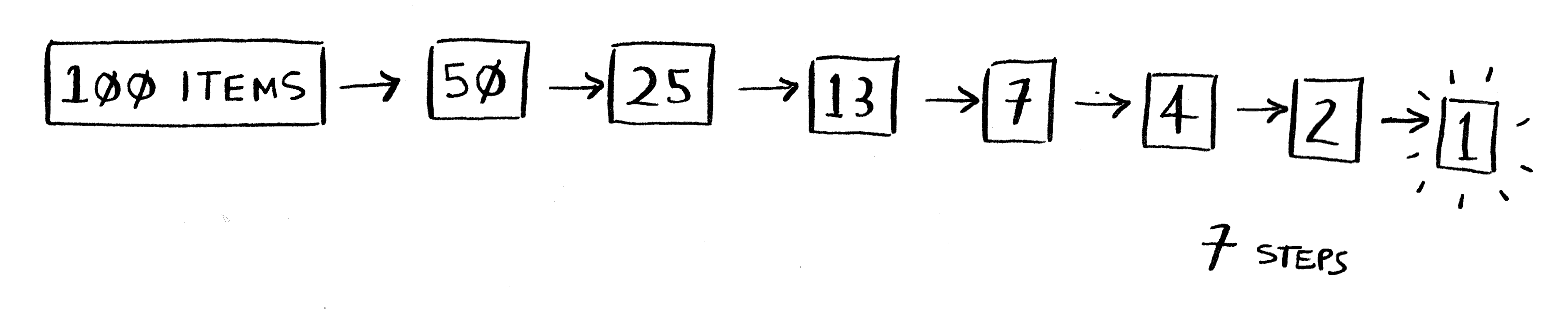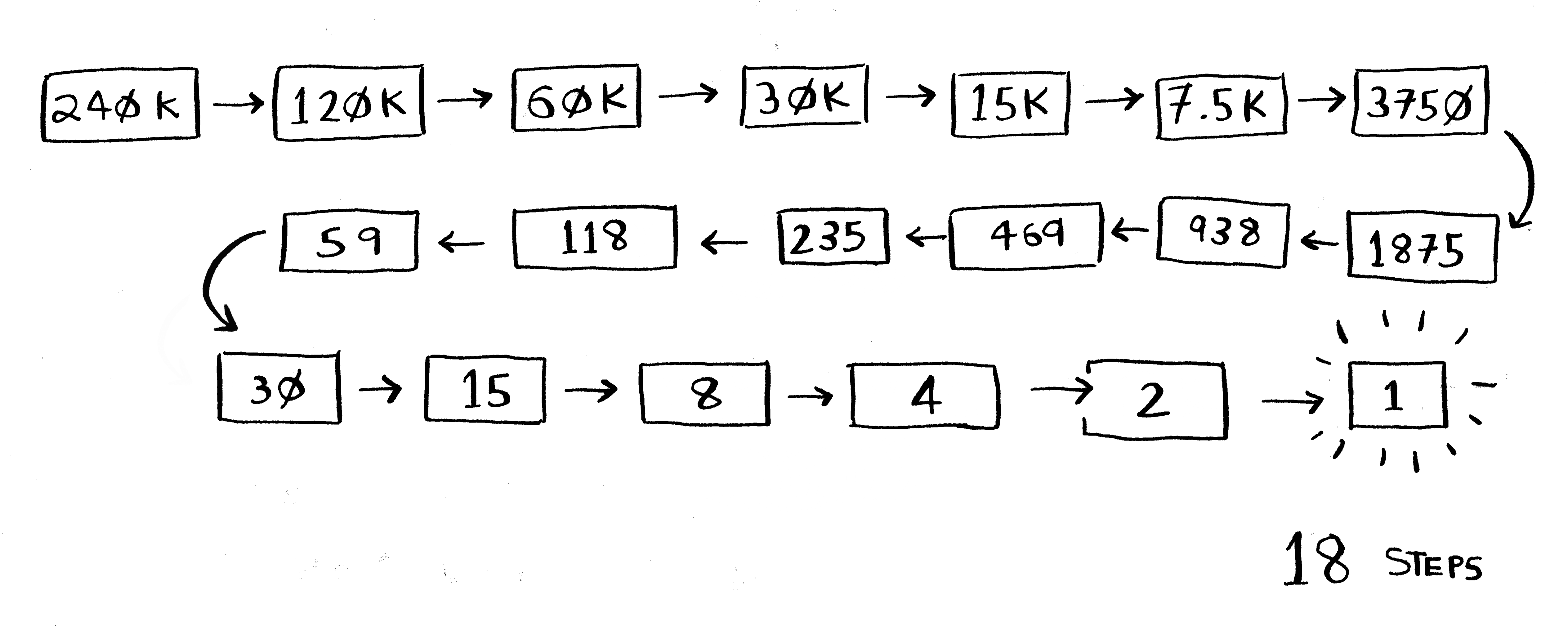كتاب استيعاب الخوارزميات، الفصل الأول، الدرس الأول
هل فكّرت يومًا كيف تُعرض لك منشورات مواقع التواصل حسب اهتماماتك؟
تبحث عن شيء في فيسبوك؟ تتوقف قليلًا أمام منشور؟
استعد إذًا لسيلٍ من المنشورات والإعلانات المرتبطة بذلك الموضوع!
تشاهد مقطعًا عن الأكل؟ ستُغرقك المنصة بمقاطع مشابهة!
بل حتى إنك تتحدث مع صديقك عن موضوع ما،
فتُفاجأ بأن المنصات تعرض عليك محتوى وإعلانات ذات صلة…
هل يقرأون أفكارك؟ هل هو سحر؟
كل ذلك يحدث باستخدام خوارزميات ذكية، برمجها مبرمجون بعناية:
إذا فعل المستخدم وتوقف عند منشور معين لعدة ثوانٍ….. فاعرض له كيت وكيت.
خلف كل نقرة، وكل توقف، وكل إعجاب، هناك خوارزمية تراقب وتتعلم.
ما هي الخوارزميات؟ وماذا تفعل بالضبط؟
-
تحلل سلوكك وكل شيء عنك.
-
تستنتج اهتماماتك حتى دون أن تضغط “إعجاب”.
-
تعرض لك محتوى يُرجّح أنك ستحبه.
-
وفي النهاية: تسهّل بيع الإعلانات لك!
نعم، كل شيء تنشره عن نفسك – حتى دون قصد – يُستخدم لتعليم وتدريب الذكاء الاصطناعي وتعزيز قدرات هذه الخوارزميات. فهي العمود الفقري للذكاء الاصطناعي الذي نراه اليوم!
ما أهمية الخوارزميات للمبرمجين؟ لماذا تهمك كمبرمج؟
-
تنمّي طريقة تفكيرك وكتابتك للرِمَاز البرمجي الكود code.
-
تنظّم الأفكار وتسلسل الخطوات.
-
تُسهّل حل المشكلات المعقدة بفعالية وبأقل المصادر،
وهذا بالضبط ما تبحث عنه الشركات اليوم.
ولهذا السبب تُدرّس الخوارزميات كأحد أهم الأساسات في تخصص علوم الحاسوب. دون فهم الخوارزميات سيصعب على المبرمج فهم وكتابة البرامج، فتصبح مهمة كتابة برنامج سريع لحل مشكلة بأفضل طريقة مهمة شاقة وصعبة، بل ومستحيلة!
لماذا أكتب هذه المقالات؟
لقلة المصادر العربية التي تشرح الخوارزميات وأساسياتها التي يحتاجها المبرمج بتدرج ويسر، فقد قررت شرح كتاب أعجمي نفيس يُعدُّ مدخلًا رائعًا لدراسة الخوارزميات، بلغة عربية لمن لا يُجيد الإنگليزية.!
ولهذا سأبدأ شرح كتاب رائع اسمه:
“Grokking Algorithms – استيعاب الخوارزميات”
وسأقدمه بالعربية، مدعومًا بالأمثلة والرسومات، بلغة مبسطة، وكل مقالة تتناول موضوعًا أو أكثر، حتى ننتهي من الكتاب، وهذه المقالات ستغنيك عن قراءة الكتاب.
المتطلبات الأساسية
-
معرفة بلغة برمجة واحدة على الأقل (مثل Python أو C) أو أي لغة أخرى، لكن الأمثلة المضروبة في الكتاب مكتوبة بلغة Python لكني سأضيف أيضًا أمثلة بلغة C.
-
إلمام بعمليات رياضية بسيطة (جمع، طرح، ضرب، قسمة، وأيضًا الأسس)، وكلما أحتجنا لمفهوم رياضي فإني سأشرحه لك قبل البدء في الدرس، كما سأفعل اليوم بشرح الأسيس (تعريب كلمة اللوغارثيم logarithm).
-
المقالات ستكون مفهومة لأي مبتدئ لديه حماس للتعلم.
قبل أن نبدأ…
تذكر أن العالم المسلم محمد بن موسى الخوارزمي
هو أول من وضع أسس علم الخوارزميات،
ولذلك نُسبت الكلمة الإنجليزية “Algorithm” إلى اسمه.
مستعد؟ لنبدأ الرحلة معًا نحو فهم الخوارزميات!
فلنتوكل على الله… ونبدأ هيا هيا بنا…
📘 الأسيس: هل تتذكر الأسس؟
🔢 الأس هو عدد المرات التي يضرب فيها الأساس في نفسه، مثلًا الرقم 5²، يُقرأ خمسة أس اثنين، ورقم خمسة هو الأساس، واثنين أس خمسة يعني ضرب الرقم خمسة في نفسه مرتين مثلًا:
أي أن:
-
الأساس = 5 الأس = 2 النتيجة = 25
مثال آخر فإن 10³ يساوي:
✅ إذن:
-
5² = 25 -
10³ = 1000
🧠 حل هذه الأمثلة قبل مواصلة القراءة:
-
8³ = ? -
4² = ? -
5³ = ? -
9² = ?
💡 ما هو الأسيس (اللوغاريثم – logarithm)؟
❓ هو فقط شكل آخر من أشكال الأس!
✏️ التعريف الرسمي:
الأسيس (لوغاريثم) أي عدد لأساس معلوم هو الأس الذي يُرفَع له الأساس المعلوم كي يعطينا العدد.
🎯 إذا فهمت التعريف، ممتاز!
وإذا لم تفهم، فلا تقلق… تابع الشرح 👇
🔢 تذكر هذا المعادلة جيدًا:
لنطبق التعريف على المعادلة المذكورة آنفًا:
أسيس العدد 25 (لأن العدد في معادلتنا هو 25)، للأساس المعلوم 5 (لأن الأساس في معادلتنا هو 5)، هو الأس الذي يُرفَع له الأساس المعلوم (أي 5) كي يعطينا العدد (أي العدد 25)،
نريد أن نعرف ما هو الأسيس (اللوغاريثم) هنا؟:
إذن ما الأس الذي إذا رفعناه للأساس 5 يعطينا 25؟
📌 عليك نور، الإجابة: 2 لأن 5² = 25
هل فهمت الآن لماذا قلت إن الأسيس هو صورة مختلفة للأس فقط؟
فنحن نحاول إيجاد الأس الموضوع فوق الرقم 5 الذي سيعطينا (إذا ضربنا الرقم 5 في نفسه حسب الأس الموضوع) العدد 25 فقط.
وبعبارة أسهل وأوضح، فنحن نقول: ما الأس الذي إذا رفعناه للأساس 5 سيعطينا العدد 25؟
والجواب سيكون: الرقم اثنين، فإن 5×5 يساوي 25.
💬 ولكتابة الأسيس بصيغة رياضية فإنه يمثل بالعربية بالرمز (لو)::
-
نقرأها: أسيس العدد 25 للأساس المعلوم 5.
-
أي: ما الأس الذي يُرفَع له الرقم 5 ليعطينا 25؟ الجواب = 2
💡 تذكر:
🔤 “لو” = وغاريثم logarithm، وهي كلمة أعجمية عُرِّبت إلى أسيس، ولكن ساد وغلب المصطلح الأعجمي لوگاريثم logarithm، ومنه أُخِذَ (لو).
🧮 اللوغاريتم هو مجرد طريقة للبحث عن الأس الذي ينتج عددًا معينًا عند رفع الأساس له.
🔍 مثال آخر: حل المسألة التالية:
أي:
يُقرَأ: أسيس العدد 8 للأساس المعلوم 2، يساوي كم؟
أي: ما الأس الذي إذا رفعناه للرقم 2 سيعطينا العدد 8؟
✅ الحل سيكون الأس: 3 لأن 2³ = 8
فلو رفعنا الأساس 2 للرقم 3 فإنه سيعطينا العدد 8، لأن ضرب الرقم 2 في نفسه ثلاث مرات (2×2×2) يساوي 8:
ويقرأ: أسيس (لوغاريثم) العدد ٨ للأساس المعلوم ٢ يساوي ٣.
🧠 أسئلة لاختبار فهمك
❓ أ. أي من الاختيارات الأربعة يعادل 32 = 2⁵:
✅ اختر الحل الصحيح:
-
1.
لو2 (32) = 5 -
2.
لو5 (2) = 35 -
3.
لو32 (5) = 2
❓ ب. أي من الاختيارات الأربعة يعادل 125 = 5³:
✅ اختر الحل الصحيح:
-
1.
لو3 (125) = 5 -
2.
لو5 (125) = 3 -
3.
لو125 (5) = 3
❓ ج. اكتب لو4 (16) = 2 بصيغة أُسية:
✅ الجواب:؟؟؟
❓ د. اكتب لو2 (64) = 6 بصيغة أُسية:
✅ الجواب:؟؟؟
❓ هـ. حل المسائل التالية:
| المسألة | الحل |
|---|---|
لو6 (36) = ? |
؟ |
لو3 (27) = ? |
؟ |
لو4 (4) = ? |
؟ |
لو1 (5) = ? |
؟ |
📘 ملاحظة أخيرة:
الأساس في اللوغاريثم يجب أن يكون أكبر من صفر و لا يساوي 1.
 ما هي الخوارزمية؟
ما هي الخوارزمية؟
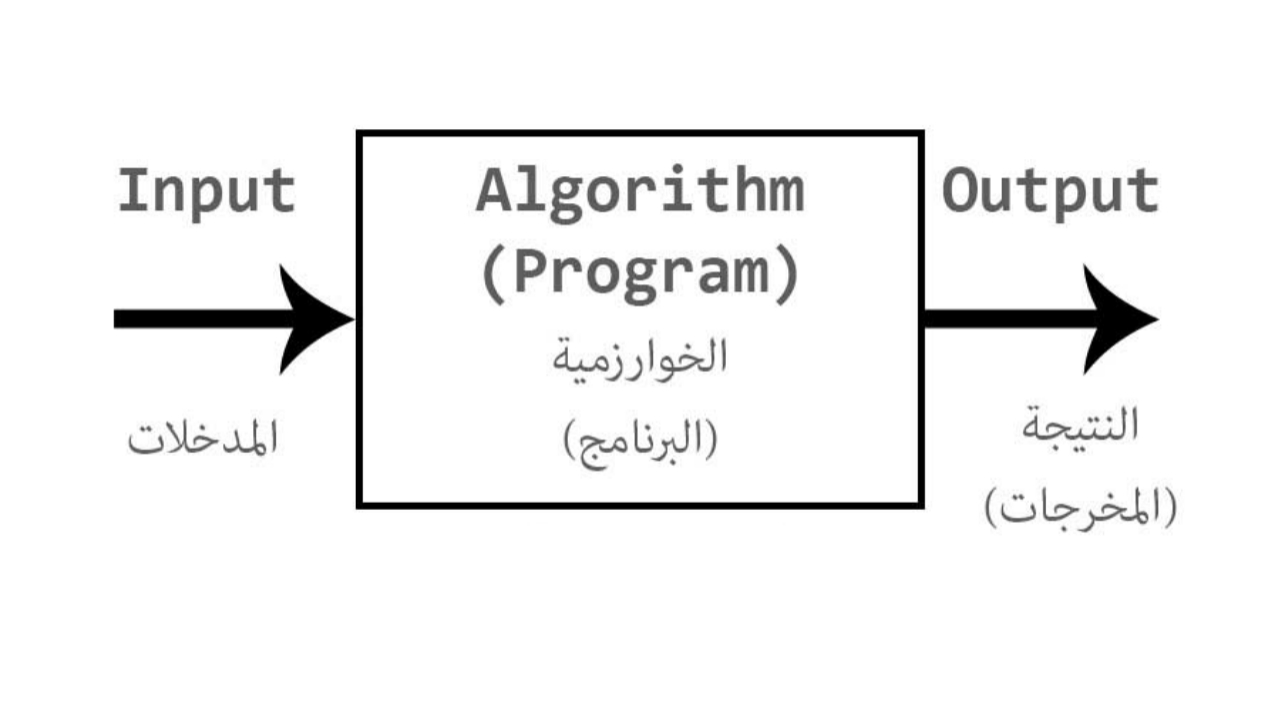
الخوارزمية: مجموعة الخطوات الدقيقة والمنطقية والمتسلسلة لحل مشكلة ما.
يمكن القول إن كل تعليمة برمجية تمثل جزءًا من خوارزمية، لأن الرِِمَاز البرمجي كاملًا ليس إلا خوارزمية لحل مشكلة معينة.
❗ كلمة “خوارزمية” في ذاتها لا توضّح معناها مباشرة، لذا عرفناها أولًا.
🧑🏫 أصل الكلمة:
- الخوارزمية مشتقة من اسم العالِم المسلم محمد بن موسى الخوارزمي (780م – 850م)، وهو عالِم رياضيات وفلك مسلم وهو أول من ابتكرها في القرن التاسع الميلادي.
- تعدَّدت إسهامات الخوارزمي وانتشرت على نطاق واسع. فمصطلح «الجبر» مشتقٌّ من العنوان العربي لأكثرِ كتبه تأثيرًا وهو كتاب «المختصر في حساب الجبر والمقابلة» بالإنجليزية: Algebra.
📚 كلمة Algorithm:
- أُدخل اسم الخوارزمي إلى اللغة اللاتينية وصار Algorismus والذي أصبح يشير إلى طريقة الحساب العددي باستخدام الأعداد العشرية. تأثَّر المصطلح اللاتيني Algorismus بالكلمة اليونانية arithmos وتعني «العدد» (مثل كلمة arithmetic وتعني علم الحساب)، ومِن ثُم أصبحت algorithm بمعنى خوارزمية، وظلت تشير إلى العمليات الحسابية العشرية، قبل أن تكتسب معناها الحديث في القرن التاسع عشر.
🧠 الخوارزميات في الحياة اليومية
مثلًا: عندما تُعدُّ كأس قهوة ☕ فإن الخطوات الدقيقة والمتسلسة لتحضير القهوة تسمى → خوارزمية.
👕 غسل الملابس، 🚪 فتح الباب، وحتى 📱 تسجيل الدخول لموقع ما… كلها خوارزميات تُنفذ بشكل تلقائي في حياتنا اليومية.
🔍 خوارزمية البحث الثنائي Binary Search والخطي
🎯 المشكلة: البحث عن عنصر (مثل اسم شخص) داخل قائمة.
مثال عملي:
لنفترض أنك ترغب بالبحث عن شخص اسمه “كمال” في دليل الهاتف القديم:
- بدلًا من تقليب الصفحات من البداية (1، 2، 3…) صفحة صفحة لتصل إلى حرف الكاف،
- قد تفتح من النصف آملًا أن تكون قريبًا من حرف الكاف، فهذا أسهل وأسرع.
- هذا بالضبط ما تفعله خوارزمية البحث الثنائي.
ولنفترض أنك تبحث عن معنى كلمة قاتل في المعجم الوسيط، فأنك لن تفتحه وتبدأ بالبحث عن الكلمة في كل صفحة حتى تصل إليه، فإن قاتل من الجذر قَتَلَ، فستفتح باب حرف القاف مباشرةً إن كنت تعرف صفحته، ولكن ردة الفعل الطبيعية أن تفتح المعجم من منتصفه لترى هل أنت قريب من حرف القاف؟
إن كان حرف القاف بعيدًا فأنك ستستمر بنفس الحركة السابقة، أن تفتح المعجم الوسيط من منتصفه المتبقي مرة أخرى، وهذا يختصر عليك الجهد والوقت، وأقصد من منتصفه المتبقي المنتصف الذي يتواجد به حرف القاف، فإن فتحت المعجم من منتصفه وكان الحرف الذي أمامك حرف السين فأنك ستفتحه مجددًا من الحروف التالية، التي تلي حرف السين.
👨💻 ولنفترض أنك تسجل للدخول إالى حسابك في الفيسبوك:
- فإن الفيسبوك سيتحقق من وجود حسابك على الموقع بالبحث عنه في قاعدة بياناته. لو كان اسم مستخدمك هو سعيد Saed فهل تتوقع أن يبدأ بالبحث عنه من البداية من حرف الألف A حتى آخر حرف Z وهو الذي يمتلك مستخدمين يصل عددهم إلى آلاف مؤلفة؟! من المنطقي أن يبدأ بالبحث عنه في مكانٍ ما في الوسط، فهذا أسرع وأسهل.
- مما سبق يتضح لك أن ما واجهناه يسمى مشكلة بحث، وكل الافتراضات السابقة تستخدم نفس خوارزمية البحث لحل المشكلة: خوارزمية البحث الثنائي binary search 🔍
سميت بخوارزمية البحث الثنائي لأنها تقسم الائحة المراد البحث داخلها عن عنصر ما إلى نصفين مرارًا وتكرارًا حتى تجد العنصر المطلوب.
⚙️ كيف تعمل خوارزمية البحث الثنائي؟
- تأخذ لائحة مرتبة من العناصر (sorted list).
- تقسمها إلى نصفين.
- تقارن العنصر في المنتصف بما تبحث عنه.
- تكرر العملية حتى تجد العنصر أو تصل لنقطة النهاية.
📌 إن وُجد العنصر → تُعيد موقعه حيث يُخزَّن.
📌 إن لم يُوجد → تُعيد قيمة فارغة أو خالية: null.
أظنك فهمت القيمة الفارغة null بما أنك مبرمج.
مثلًا لو وجدت خوارزمية البحث الثنائي اسم سعيد “مش سعيد الزعزعي” فإنها ستعيد موقعه حيث يُخزَّن، لنفترض أن موقعه 1400، أما إن لم تجده فإنها سترجع قيمة فارغة null.
🎮 لنلعب لعبة!
سأفكر برقم محصور بين الواحد والرقم مائة، وأنت ستخمن الرقم في أسرع محاولات ممكنة. في كل تخمين ستقوله سأخبرك إذا كان الرقم الذي خمنته:
- صحيحًا ✅
- أو يكبر الرقم الذي أفكر به (too high)
- أو يصغره (too low)
البحث البدائي (الخطي)
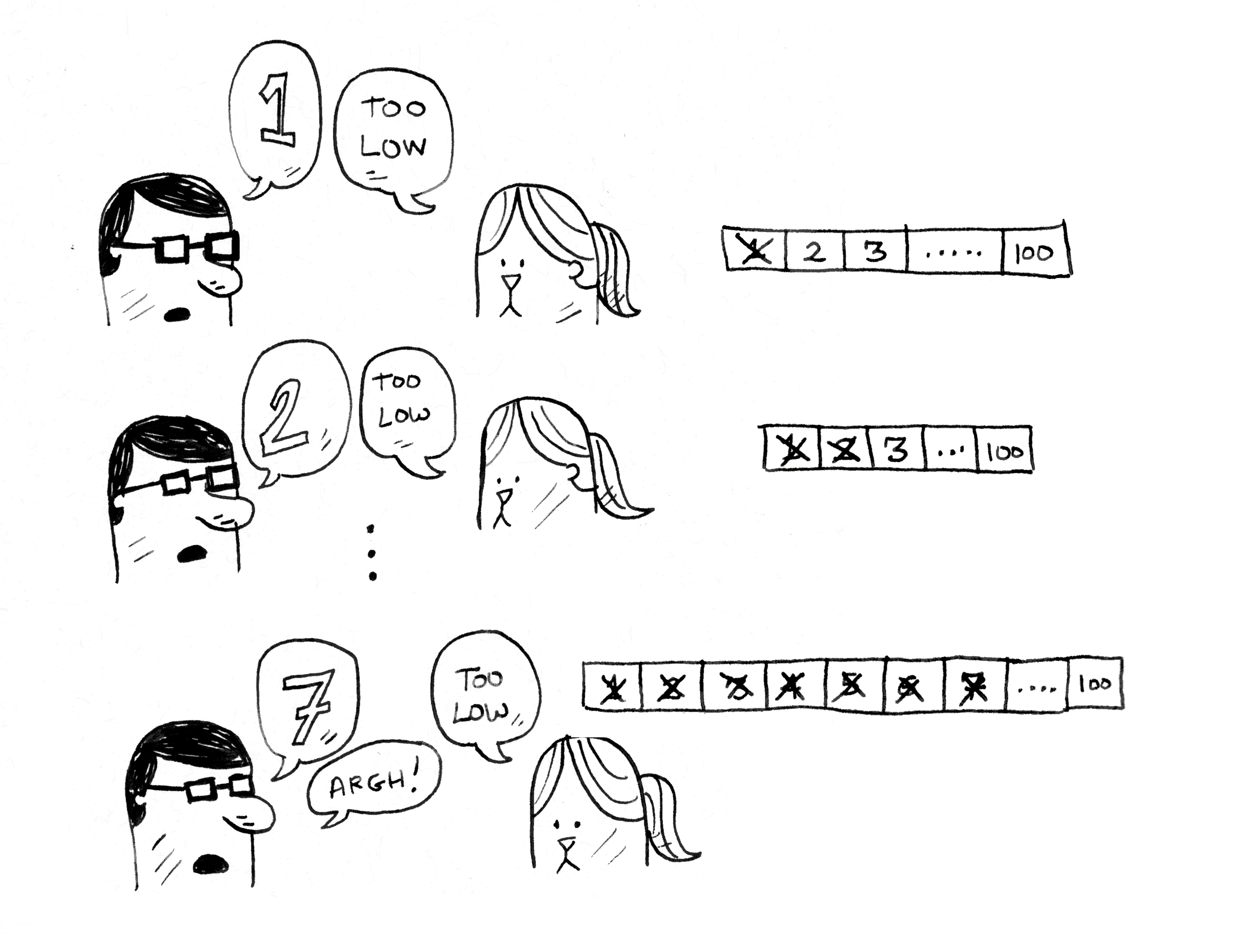
سأفترض أنك أردت أن تتذاكى عليَّ وخمنت بالطريقة البدائية التقليدية هكذا:
واحد، اثنان، ثلاثة، أربعة، خمسة، إلخ…
يبدو كالرسومات التالية:
- تقول: واحد؟
أجيبك: لا، بل يكبره. - تقول: اثنان؟
أجيبك: لا، بل يكبره.
الطريقة التي استعملتَها في تخمين الرقم الذي أفكر به رقمًا رقمًا تسمى خوارزمية البحث البدائي أو البحث الخطي (Linear Search).
هذه الخوارزمية بطيئة، لأنك محدود برقم واحد في كل تخمين، وقد تحتاج إلى 99 محاولة إذا كان الرقم 99! أليس هذا متعبًا؟
❌ لن ألعب معك إن كنت ستضيع الوقت هكذا!
البحث الثنائي (Binary Search)
لنتبادل الأدوار في اللعب، أنت تفكر برقم وأنا أخمنه. سأريك كيف أن خوارزمية البحث الثنائي binary search أسرع بكثير.
لنفترض أن الرقم الذي تفكر به هو 57:
- سأبدأ بتقسيم اللائحة المرتبة من 1 إلى 100 إلى نصفين → أبدأ بـ 50
- أقول: أهو الرقم 50؟
تُجيب: خطأ، يكبره.
- أقول: أهو الرقم 50؟
- أتخلص من كل الأرقام من 1 إلى 50
الآن أجرب 75- أقول: أهو الرقم 75؟
تُجيب: خطأ، يصغره.
- أقول: أهو الرقم 75؟
- الآن بين 50 و75 → أجرب 63
- أقول: أهو الرقم 63؟
تُجيب: خطأ، يصغره.
- أقول: أهو الرقم 63؟
- بين 50 و63 → أجرب 57
- أقول: أهو الرقم 57؟
تُجيب: أحسنت، صحيح! الرقم الذي ينتصف الأرقام بين 63 و50 هو 57!
- أقول: أهو الرقم 57؟
🎉 هنيئًا لك!
ها أنت تعلمت أول خوارزمية بحثك الأولى: خوارزمية البحث الثنائي
لا يهم أي رقم فكرت به حتى وإن كان الرقم مائة 100، فإني سأخمنه بتخمينات أقصاها سبعة تخمينات فحسب.
سأبدأ التخمين من الرقم مائة، من النهاية، والرقم الذي أفكر به هو الرقم واحد، انظر كم سيأخذ الأمر مني محاولات،7 سبعة تخمينات فقط:
مثال ثانٍ: القاموس
لنقل أنك تبحث عن كلمة في قاموس فيه 240,000 كلمة.
في أسوأ حالة worst case، وأسوأ حالة أن تكون الكلمة في نهاية القاموس (اللائحة)، كم خطوة ستأخذ كل خوارزمية بحث من خوارزميتي البحث الثنائي والبدائي لإيجاد كلمة ما في القاموس الذي عدد كلماته 240,000 كلمة؟
ستأخذ خوارزمية البحث البدائي 240,000 خطوة إذا كانت الكلمة في نهاية القاموس، لكن في خوارزمية البحث الثنائية ستقسم عدد الكلمات إلى نصفين، وهكذا سننتهي بالكلمة المطلوبة، وستأخذ خوارزمية البحث الثنائية 18 خطوة فقط!
| الخوارزمية | أسوأ حالة (Worst Case) |
|---|---|
| البحث البدائي | 240,000 خطوة |
| البحث الثنائي | 18 خطوة فقط |
أليس الفرق شاسعًا بينهما؟ 🔥
ماذا لو الرقم ضخم جدًا (Million) ؟
أظنك تتساءل لو كان لديك رقم ضخم، لنقل ألف ألف رقم (million)، هل ستأخذ الورقة والقلم وتبدأ بتقسيمه كل مرة إلى نصفين لتعرف عدد الخطوات؟
أبدًا لا، هنا يأتي دور الرياضيات ✨ وتحديدًا ما تعلمته في بداية الدرس، أنه الأسيس!
القاعدة:
لأي لائحة حجمها س، فإن:
- خوارزمية البحث الثنائي تحتاج إلى لو2(س) خطوة (في أسوأ حالة) in the worst case>
- خوارزمية البحث البدائي تحتاج إلى س خطوة في أسوأ حالة.
استعمل الآلة الحاسبة لإيجاد حل المسألة الرياضية السابقة (لو2 (س)).
يرجى الإنتباه، سيكون الأساس للأسيس دائمًا هو 2، فإني في بقية المقالات سأستعمل (لو) متبوعًا بحجم اللائحة، ولن أكتب الأساس 2. لكن لماذا الأساس المعلوم هو الرقم 2؟
لأن الحاسوب لا يفهم إلا الآحاد والأصفار، نظام العد الثنائي binary system فقط الذي أساسه الرقم 2.
“الحاسوب يفهم فقط النظام الثنائي (0 و 1)، لذا الأساس هو دائمًا 2”
لنحاول تطبيق القاعدة:
لديك لائحة عدد عناصرها 1024 عنصرًا ، إذا طبقنا القاعدة فإن:
لو (1024) = 10
أتفقنا مسبقًا أن الأساس سيكون دائمًا الرقم 2 ولن أكتبه في بقية الدروس القادمة.
تمثيل خوارزمية البحث الثنائي برمجيًا
حان الوقت لنبرمج أول خوارزمية بحث تعلمتها. سنحتاج في رِمَازنا البرمجي إلى الصفيفَات (arrays)، إن كنت لا تعلم ماهيتها فلا تقلق، فإني سأشرحها في الفصل الثاني من الكتاب.
المطلوب منك فهمه عن الصفيفة (array) أنها متتالية من عناصر من نفس نوع البيانات، في مواقع ذاكرة متجاورة.
الفهرسة تبدأ في الصفيفة من الرقم صفر، فموقع أول عنصر فيها يمثل بالرقم صفر، وثاني عنصر بالرقم واحد، وهكذا…
سننشئ وظيفة (function) ونسميها binary_search تأخذ صفيفة مرتبة (sorted array) وعنصر. فإن كان العنصر الذي أخذته الوظيفة موجودًا في الصفيفة التي استقبلتها فإنها سترجع موقعه، وإن لم يكن موجودًا سترجع قيمة فارغة null.
أولًا علينا معرفة طول المصفوفة، لنحدد الرقم الذي تبدأ منه والرقم الذي تنتهي عنده:
تحديد البداية والنهاية:
low = 0
high = len(list) – 1الآن بعدما حددنا بدايتها ونهايتها علينا تقسيمها إلى نفصين في كل مرة، ثم نخزن العنصر الذي ينتصف الصفيفة في متغير لمقارنته لاحقًا:
mid = (low + high) / 2
guess = list[mid]الآن علينا اختبار العنصر الذي خزناه بالعنصر المعطى عند استدعاء الوظيفة، هل يساويه أم يصغره أو يكبره.
if guess < item:
low = mid + 1
🐍 هذا الرِمَاز البرمجي كاملًا مكتوب بلغة Python:
def binary_search(lis, item):
low = 0
high = len(lis) - 1
while low <= high:
# … check the middle element
mid = (low + high) // 2
guess = lis[mid]
# Found the item.
if guess == item:
return mid
# The guess was too high.
if guess > item:
high = mid - 1
# The guess was too low.
else:
low = mid + 1
# Item doesn’t exist
return None
my_list = [1, 3, 5, 7, 9]
print(binary_search(my_list, 3))
print(binary_search(my_list, -1))
🖥️ هذا رِمَاز برمجي مكتوب بلغة C:
#include <stdio.h>
int binarySearch(int[], int, int);
int main()
{
int myList[] = {1, 3, 5, 7, 9};
int len = sizeof(myList) / sizeof(myList[0]);
printf("%d\n", binarySearch(myList, 3, len)); // 1
printf("%d\n", binarySearch(myList, -1, len)); // -1
return 0;
}
int binarySearch(int list[], int item, int len)
{
int low = 0;
int high = len - 1;
while (low <= high)
{
int mid = (low + high) / 2;
int guess = list[mid];
if (guess == item)
{
return mid;
}
else if (guess > item)
{
high = mid - 1;
}
else
{
low = mid + 1;
}
}
return -1; // number not found
}
📝 تمارين
- عندك لائحة مرتبة من 128 اسمًا، فقررت أن تبحث فيها عن اسم ما باستخدام خوارزمية البحث الثنائي، فما أقصى (أي: أسوأ حالة) عدد من الخطوات تحتاجها للعثور عليه؟
- ضاعفت اللائحة السابقة، أي ضعف العدد 128، فما أقصى عدد من الخطوات تحتاجها للعثور على الاسم؟
💡عليك حلها!
الخاتمة
لن تكون هنا نهايتنا بل بدايتنا لسلسلة متكاملة وشاملة عن الخوارزميات، وسأشرح الكتاب كاملًا، وستغنيك المقالات المنشورة عنه عن قراءته.
وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.
تابعنا على مواقع التواصل الاجتماعي
كتاب استيعاب الخوارزميات، الفصل الأول، الدرس الأول

ألم تفكر كيف تعرض لك مواقع التواصل الاجتماعي المنشورات حسب اهتمامك؟
تبحث عن شيء في الفيسبوك أو تتوقف قليلًا للنظر في منشور ما عليه فتجده قد عرض لك منشورات وإعلانات عن ذلك الشيء. تشاهد مقطعًا ما عن الأكل فتجده قد عرض عليه مقاطع ومنشورات وإعلانات عن الأكل!
كل ذلك يحدث بخوارزمية برمجها مبرمج وهي مصممة لعرض المنشورات التي تهمك، تحلل كل شيء عنك لعرض المنشورات لك، مثلًا إذا فعل المستخدم كذا وكذا، وإذا توقف هنا لمدة كذا وكذا، فافعل كيت وكيت…
كل شيء تنشره عن نفسك يستخدم لتعليم الذكاء الاصطناعي وتعزيز الخوارزميات لعرض الإعلانات لك. الخوارزميات العمود الفقري للذكاء الاصطناعي الذي نراه اليوم!
الخوارزميات لا بُدَّ منها للمبرمج، فإنها:
1. تحسن طريقة تفكيره، وكتابته للرِمَاز البرمجي code.
2. وتساعد على وضوح الأفكار وتنظيمها.
3. وحل المشكلات المعقدة بفعالية وبأقل المصادر، والأخير ما تبحث عنه الشركات.
الخوارزميات تُدرَّس في الجامعات للطلبة في علوم الحاسوب. دون فهم الخوارزميات سيصعب على المبرمج فهم وكتابة البرامج، فتصبح مهمة كتابة برنامج سريع لحل مشكلة بأفضل طريقة مهمة شاقة وصعبة، بل ومستحيلة!
لقلة المصادر العربية التي تشرح الخوارزميات وأساسياتها التي يحتاجها المبرمج بتدرج ويسر، فقد قررت شرح كتاب أعجمي نفيس يُعدُّ مدخلًا رائعًا لدراسة الخوارزميات، بلغة عربية لمن لا يُجيد الإنگليزية.
الكتاب يشرح الخوارزميات بسهولة وبرسومات تسهل الفهم، اسم الكتاب «استيعاب الخوارزميات Grokking Algorithms»، وسأشرحه بمقالات منفصلة، كل مقالة تتناول موضوعًا أو أكثر، حتى ننتهي من الكتاب، وهذه المقالات ستغنيك عن قراءة الكتاب.
متطلبات الدورة
كل ما تحتاجه للبدء معرفة بأساسيات لغة برمجية، مثل لغة Python أو C أو أي لغة أخرى، لكن الأمثلة المضروبة في الكتاب مكتوبة بلغة Python لكني سأضيف أيضًا أمثلة بلغة C.
أما المعرفة الرياضية فتكفي معرفة الأساسيات من ضرب وقسمة وطرح وجمع، وأيضًا الأسس، وكلما أحتجنا لمفهوم رياضي فإني سأشرحه لك قبل البدء في الدرس، كما سأفعل اليوم بشرح الأسيس (تعريب كلمة اللوغارثيم logarithm).
نتوكل على الله ونبدأ!
الأسيس
هل تتذكر الأسس؟
الأس هو عدد المرات التي يضرب فيها الأساس في نفسه، مثلًا الرقم 5²، يُقرأ خمسة أس اثنين، ورقم خمسة هو الأساس، واثنين أس خمسة يعني ضرب الرقم خمسة في نفسه مرتين:
5×5 = 25
إذن فإن خمسة أس اثنين 5² يساوي 25، وبالمثل فإن 10³ يساوي:
10x10x10 = 1000
إذن فإن عشرة أس ثلاثة يساوي ألف (10³ = 1000).
حل هذه الأمثلة قبل مواصلة القراءة:
8³ = ?
4² = ?
5³ = ?
9² = ?
حسنًا، ما الأسيس (اللوغاريثم logarithm)؟
هو صورة مختلفة للأس فقط!
التعريف يقول: أسيس (لوغاريثم) أي عدد لأساس معلوم هو الأس الذي يُرفَع له الأساس المعلوم كي يعطينا العدد.
إن فهمت التعريف فخير وبركة وإن لم تفهمه فتابع الشرح.
تذكر هذا المعادلة جيدًا:
5² = 25
لنطبق التعريف على المعادلة المذكورة آنفًا (5² = 25):
أسيس العدد 25 (لأن العدد في معادلتنا هو 25)، للأساس المعلوم 5 (لأن الأساس في معادلتنا هو 5)، هو الأس الذي يُرفَع له الأساس المعلوم (أي 5) كي يعطينا العدد (أي العدد 25)، إذن ما هو الأس الذي إذا رفعنا الأساس 5 إليه أعطانا العدد 25؟
عليك نور، هو الأس 2، فلو رفعنا الأساس 5 إلى الأس 2 فإن العدد الذي سنحصل عليه هو العدد 25.
هل فهمت الآن لماذا قلت إن الأسيس هو صورة مختلفة للأس فقط؟
فنحن نحاول إيجاد الأس الموضوع فوق الرقم 5 الذي سيعطينا (إذا ضربنا الرقم 5 في نفسه حسب الأس الموضوع) العدد 25 فقط.
وبعبارة أسهل وأوضح، فنحن نقول: ما الأس الذي إذا رفعناه للأساس 5 سيعطينا العدد 25؟
والجواب سيكون: الرقم اثنين، فإن 5×5 يساوي 25.
ولكتابة الأسيس بصيغة رياضية فإنه يمثل بالعربية بالرمز (لو):
لو5 (25) = 2
وبصيغة إنگليزية:
log5 (25) = 2
ونقرأه: أسيس العدد 25 للأساس المعلوم 5. فإن العدد هو 25، والأساس المعلوم هو 5.
لو: لوغاريثم logarithm، وهي كلمة أعجمية عُرِّبت إلى أسيس، ولكن ساد وغلب المصطلح الأعجمي لوگاريثم logarithm، ومنه أُخِذَ (لو).
مثال آخر:
حل المسألة التالية:
لو2 (8) = ؟
log2(8) = ?
يُقرَأ: أسيس العدد 8 للأساس المعلوم 2، يساوي كم؟
أي: ما الأس الذي إذا رفعناه للرقم 2 سيعطينا العدد 8؟
الحل سيكون الأس 3، فلو رفعنا الأساس 2 للرقم 3 فإنه سيعطينا العدد 8، لأن ضرب الرقم 2 في نفسه ثلاث مرات (2×2×2) يساوي 8:
log2 (8) = 3
لو2 (8) = 3
ويقرأ: أسيس (لوغاريثم) العدد ٨ للأساس المعلوم ٢ يساوي ٣.
أسئلة لاختبار فهمك:
أ. أي من الاختيارات الأربعة يعادل 32 = 2⁵:
1. لو2 (32) = 5
2. لو5 (2) = 35
3. لو32 (5) = 2
ب. أي من الاختيارات الأربعة يعادل 125 = 5³:
1. لو3 (125) = 5
2. لو5 (125) = 3
3. لو125 (5) = 3
ج. اكتب لو4 (16) = 2 بصيغة أسيَّة.
د. اكتب لو2 (64) = 6 بصيغة أسيَّة.
هـ. حل المسائل التالية:
لو6 (36) = ؟
لو3 (27) = ؟
لو4 (4) = ؟
لو1 (5) = ؟
الخوارزمية

الخوارزمية: مجموعة الخطوات الدقيقة والمنطقية المتسلسلة لحل مشكلة ما.
يمكن تسمية كل تعليمة من الرِمَاز البرمجي بخوارزمية، لأن الرِِمَاز البرمجي كاملًا ليس إلا خوارزمية لحل مشكلة ما.
كلمة «خوارزمية» في ذاتها لا توضِّح معناها لهذا عرفتها في البداية. الخوارزمية مشتقة من اسم محمد بن موسى الخوارزمي (من عام ٧٨٠ إلى عام ٨٥٠ تقريبًا)، وهو عالِم رياضيات وفلك مسلم وهو أول من ابتكرها في القرن التاسع الميلادي.
تعدَّدت إسهامات الخوارزمي وانتشرت على نطاق واسع. فمصطلح «الجبر» مشتقٌّ من العنوان العربي لأكثرِ كتبه تأثيرًا وهو كتاب «المختصر في حساب الجبر والمقابلة».
أُدخل اسم الخوارزمي إلى اللغة اللاتينية وصار Algorismus والذي أصبح يشير إلى طريقة الحساب العددي باستخدام الأعداد العشرية. تأثَّر المصطلح اللاتيني Algorismus بالكلمة اليونانية arithmos وتعني «العدد» (مثل كلمة arithmetic وتعني علم الحساب)، ومِن ثُم أصبحت algorithm بمعنى خوارزمية، وظلت تشير إلى العمليات الحسابية العشرية، قبل أن تكتسب معناها الحديث في القرن التاسع عشر.
عندما تُعدُّ كأس قهوة فإن الخطوات الدقيقة والمتسلسة لتحضير القهوة تسمى خوازرمية، فالخوارزميات نستخدمها في حياتنا اليومية بداهةً، فتح الباب وغسل الملابس وغيرهما…
خوارزمية البحث الثنائي والخطي
لنفترض أنك ترغب بالبحث عن شخص اسمه كمال في دليل الهاتف القديم، وبما أن اسمه كمال فإنك ستجد رقمه في الأسماء التي تبدأ بحرف الكاف. لن تفتح الكتاب من البداية وتبدأ بتقليب الصفحات صفحة صفحة لتصل إلى حرف الكاف، بل قد تفتح دليل الهاتف من النصف آملًا أن تكون قريبًا من حرف الكاف، فهذا أسهل وأسرع.
ولنفترض أنك تبحث عن معنى كلمة قاتل في المعجم الوسيط، فأنك لن تفتحه وتبدأ بالبحث عن الكلمة في كل صفحة حتى تصل إليه، فإن قاتل من الجذر قَتَلَ، فستفتح باب حرف القاف مباشرةً إن كنت تعرف صفحته، ولكن ردة الفعل الطبيعية أن تفتح المعجم من منتصفه لترى هل أنت قريب من حرف القاف؟
إن كان حرف القاف بعيدًا فأنك ستستمر بنفس الحركة السابقة، أن تفتح المعجم الوسيط من منتصفه المتبقي مرة أخرى، وهذا يختصر عليك الجهد والوقت، وأقصد من منتصفه المتبقي المنتصف الذي يتواجد به حرف القاف، فإن فتحت المعجم من منتصفه وكان الحرف الذي أمامك حرف السين فأنك ستفتحه مجددًا من الحروف التالية، التي تلي حرف السين.
ولنفترض أنك تسجل للدخول إالى حسابك في الفيسبوك، فإن الفيسبوك سيتحقق من وجود حسابك على الموقع بالبحث عنه في قاعدة بياناته. لو كان اسم مستخدمك هو سعيد Saed فهل تتوقع أن يبدأ بالبحث عنه من البداية من حرف الألف A حتى آخر حرف Z وهو الذي يمتلك مستخدمين يصل عددهم إلى آلاف مؤلفة؟!
من المنطقي أن يبدأ بالبحث عنه في مكانٍ ما في الوسط، فهذا أسرع وأسهل.
مما سبق يتضح لك أن ما واجهناه يسمى مشكلة بحث، وكل الافتراضات السابقة تستخدم نفس خوارزمية البحث لحل المشكلة: خوارزمية البحث الثنائي binary search.
سميت بخوارزمية البحث الثنائي لأنها تقسم الائحة المراد البحث داخلها عن عنصر ما إلى نصفين مرارًا وتكرارًا حتى تجد العنصر المطلوب.
خوارزمية البحث الثنائي تستقبل لائحة مرتبة من العناصر sorted list، ويجب أن تكون اللائحة مرتبة. إن كان العنصر الذي تبحث عنه في اللائحة متواجدًا فيها فإن خوارزمية البحث الثنائي سترجع موقع العنصر حيث يُخزَّن، وإن لم تجده ستعيد قيمة فارغة أو خالية null.
أظنك فهمت القيمة الفارغة null بما أنك مبرمج.
مثلًا لو وجدت خوارزمية البحث الثنائي اسم سعيد فإنها ستعيد موقعه حيث يُخزَّن، لنفترض أن موقعه 1400، أما إن لم تجده فإنها سترجع قيمة فارغة null.
لنلعب لعبة!
سأفكر برقم محصور بين الواحد والرقم مائة، وأنت ستخمن الرقم في أسرع محاولات ممكنة. في كل تخمين ستقوله سأخبرك إذ كان الرقم الذي خمنته صحيحًا أو يكبر الرقم الذي أفكر به too high، أو يصغره too low.
سأفترض أنك أردت أن تتذاكى عليَّ وخمنتَ بالطريقة البدائية التقليدية هكذا: واحد، اثنان، ثلاثة، أربعة، خمسة، إلخ…
سيبدو كالرسومات التالية:
تقول: واحد؟
أجيبك: لا، بل يكبره.
تقول: اثنان؟
أجيبك: لا، بل يكبره.
الطريقة التي استعملتَها في تخمين الرقم الذي أفكر به رقمًا رقمًا يسمى بخوارزمية البحث البدائي أو التقليدي حسب ما يسميها الكاتب في كتابه، وتسمى أيضًا خوارزمية البحث الخطية liner search، وهذه الخوارزمية بطيئة فأنك محدود برقم واحد في كل تخمين، وستحتاج إلى تسعة وتسعين مرة تخمين إن كان الرقم الذي أفكر به تسعة وتسعين، أليس هذا متعبًا؟
لن ألعب معك إن كنت ستضيع الوقت هكذا!
لنتبادل الأدوار في اللعب، أنت تفكر برقم وأنا أخمنه، سأريك كيف أن خوارزمية البحث الثنائي binary search أسرع من خوارزمية البحث البدائي simple search. لنفترض أن الرقم الذي تفكر به هو 57:
سأبدأ بتقسيم اللائحة المرتبة إلى نصفين (أتفقنا أن الرقم محصور بين الرقم واحد ومائة، إذن فإن اللائحة مرتبة!)، وسأبدأ من الرقم خمسين 50.
أقول: أهو الرقم 50؟
تُجيب: خطأ، يكبره.
انظر كيف خمنت أكثر من خمسين رقمًا في مرة واحدة، بما أنه يكبره فلا يعقل أن أعيد وأقول لك: أهو الرقم 47؟
لأني أعلم بأن الرقم الذي تفكر به يكبر الرقم 50. هيا سأكمل وأقسم الجزء المتبقي إلى نصفين مرة أخرى.
أقول: أهو الرقم 75؟
تُجيب: خطأ، يصغره!
يصغر الرقم 75 لكني تخلصت من خمسة وعشرين رقمًا في تخمين واحد!
خوارزمية البحث الثنائي تقسم الائحة مرارًا وتكرارًا إلى نصفين، وفي كل مرة تختصر نصف اللائحة. هيا، لنستمر بالتخمين، هذه المرة سأقول 63، لأن الرقم في منتصف الأرقام بين 50 و75 هو 63.
أقول: أهو الرقم 63؟
تُجيب: أخطأت، يصغره!
أقول: أهو الرقم 57؟
تُجيب: أحسنت، صحيح!
الرقم الذي ينتصف الأرقام بين 63 و50 هو 57!
هنيئًا لك، ها أنت تعلمت خوارزمية بحثك الأولى، خوارزمية البحث الثنائي!
لا يهم أي رقم فكرت به حتى وإن كان الرقم مائة، فإني سأخمنه بتخمينات أقصاها سبعة تخمينات فحسب.
اسأبدأ التخمين من الرقم مائة، من النهاية، والرقم الذي أفكر به هو الرقم واحد، انظر كم سيأخذ الأمر مني محاولات، سبعة تخمينات فقط:
مثال ثانٍ
لنفترض أنك تبحث عن كلمة في قاموس عدد كلماته 240,000 كلمة. في أسوأ حالة worst case، وأسوأ حالة أن تكون الكلمة في نهاية القاموس (اللائحة)، كم خطوة ستأخذ كل خوارزمية بحث من خوارزميتي البحث الثنائي والبدائي لإيجاد كلمة ما في القاموس الذي عدد كلماته 240,000 كلمة؟
ستأخذ خوارزمية البحث البدائي 240,000 خطوة إذا كانت الكلمة في نهاية القاموس، لكن في خوارزمية البحث الثنائية ستقسم عدد الكلمات إلى نصفين، وهكذا سننتهي بالكلمة المطلوبة، وستأخذ خوارزمية البحث الثنائية 18 خطوة فقط!
أليس الفرق شاسعًا بينهما؟
أظنك تتساءل لو كان لديك رقم ضخم، لنقل ألف ألف رقم (million)، هل ستأخذ الورقة والقلم وتبدأ بتقسيمه كل مرة إلى نصفين لتعرف عدد الخطوات؟
أبدًا لا، هنا يأتي دور الرياضيات، وتحديدًا ما تعلمته في بداية الدرس، أنه الأسيس!
القاعدة تقول: لأي لائحة من س، فإن خوارزمية البحث الثنائية ستستغرق لو2 (س) خطوة في أسوأ حالة in the worst case، أما خوارزمية البحث البدائية ستستغرق س خطوة في أسوأ حالة.
استعمل الآلة الحاسبة لإيجاد حل المسألة الرياضية السابقة (لو2 (س)).
يرجى الإنتباه، سيكون الأساس للأسيس دائمًا هو 2، فإني في بقية المقالات سأستعمل (لو) متبوعًا بحجم اللائحة، ولن أكتب الأساس 2. لكن لماذا الأساس المعلوم هو الرقم 2؟
لأن الحاسوب لا يفهم إلا الآحاد والأصفار، نظام العد الثنائي binary system فقط الذي أساسه الرقم 2.
لنحاول تطبيق القاعدة:
لديك لائحة عدد عناصرها 1024 عنصرًا، إذا طبقنا القاعدة فإن:
لو (1024) = 10
أتفقنا مسبقًا أن الأساس سيكون دائمًا الرقم 2 ولن أكتبه في بقية الدروس القادمة.
تمثيل خوارزمية البحث الثنائي برمجيًا
حان الوقت لنبرمج أول خوارزمية بحث تعلمتها. سنحتاج في رِمَازنا البرمجي إلى الصفيفَات arrays، إن كنت لا تعلم ماهيتها فلا تقلق، فإني سأشرحهها في الفصل الثاني من الكتاب.
المطلوب منك فهمه عن الصفيفة array أنها متتالية من عناصر من نفس نوع البيانات، في مواقع ذاكرة متجاورة.
الفهرسة تبدأ في الصفيفة من الرقم صفر، فموقع أول عنصر فيها يمثل بالرقم صفر، وثاني عنصر بالرقم واحد، وهكذا…
سننشئ وظيفة function ونسميها binary_search تأخذ صفيفة مرتبة sorted array وعنصر. فإن كان العنصر الذي أخذته الوظيفة موجودًا في الصفيفة التي أستقبلتها فإنها سترجع موقعه، وإن لم يكن موجودًا سترجع قيمة فارغة null.
أولًا علينا معرفة طول المصفوفة، لنحدد الرقم الذي تبدأ منه والرقم الذي تنتهي عنده:
low = 0
high = len (list) – 1
الآن بعدما حددنا بدايتها ونهايتها علينا تقسيمها إلى نفصين في كل مرة، ثم نخزن العنصر الذي ينتصف الصفيفة في متغير لمقارنته لاحقًا:
mid = (low + high) / 2
guess = list[mid]
الآن علينا اختبار العنصر الذي خزناه بالعنصر المعطى عند استدعاء الوظيفة، هل يساويه أم يصغره أو يكبره.
if guess < item:
low = mid + 1
هذا الرِمَاز البرمجي كاملًا مكتوب بلغة Python:
def binary_search(lis, item):
low = 0
high = len(lis) – 1
while low <= high:
# … check the middle element
mid = (low + high) // 2
guess = lis[mid]
# Found the item.
if guess == item:
return mid
# The guess was too high.
if guess > item:
high = mid – 1
# The guess was too low.
else:
low = mid + 1
# Item doesn’t exist
return None
my_list = [1, 3, 5, 7, 9]
print(binary_search(my_list, 3))
print(binary_search(my_list, -1))
- هذا رِمَاز برمجي مكتوب بلغة C:
#include
int binarySearch(int[], int, int);
int main()
{
int myList[] = {1, 3, 5, 7, 9};
int len = sizeof(myList) / sizeof(myList[0]);
printf(“%d\n”, binarySearch(myList, 3, len)); // 1
printf(“%d\n”, binarySearch(myList, -1, len)); //-1
return 0;
}
int binarySearch(int list[], int item, int len)
{
int low = 0;
int high = len;
while (low <= high)
{
int mid = (low + high)/2;
int guess = list[mid];
if (guess == item)
{
return mid;
}
else if (guess > item)
{
high = mid – 1;
}
else
{
low = mid + 1;
}
}
return -1; //number not found
}
تمارين
1. عندك لائحة مرتبة من 128 اسمًا، فقررت أن تبحث فيها عن اسم ما باستخدام خوارزمية البحث الثنائي، فما أقصى (أي: أسوأ حالة) عدد من الخطوات تحتاجها للعثور عليه؟
2. ضاعفت اللائحة السابقة، أي ضعف العدد 128، فما أقصى عدد من الخطوات تحتاجها للعثور على الاسم؟
عليك حلها!
الخاتمة
لن تكون هنا نهايتنا بل بدايتنا لسلسلة متكاملة وشاملة عن الخوارزميات، وسأشرح الكتاب كاملًا، وستغنيك المقالات المنشورة عنه عن قراءته.
وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.
تابعنا على مواقع التواصل الاجتماعي
شارك بتعليقك
يجب أنت تكون مسجل الدخول لتضيف تعليقاً.