السلام عليكم ورحمة الله تعالى وبركاته
هذا المقال الثاني لشرح كتاب «استيعاب الخوارزميات»، وما زلنا في الفصل الأول، وهذا الدرس الثاني منه، فقد قسَّمت فصول الكتاب إلى أجزاء، في كل مقالة نشرح فيها جزءًا.
سنبدأ شرح درس اليوم، وفي نهاية المقال نحل أسئلة الدرس السابق إن وُجِدَت لتتحقق من صحة حلك.
مقال اليوم طويل، جهز نفسك واجلس في مكانٍ هادئ مع ورقتك وقلمك ومشروبك المفضل. إن استصعبت درس اليوم فيستحسن بك دراسته على جلسات، قسمه وادرس في كل جلسة جزءًا منه، وهكذا…
العاملي
مفهوم رياضي سهل جدًا، ستفهمه سريعًا، أضمن لك!
يسمى العاملي أو المضروب، وعاملي العدد س يساوي ضرب كل الأرقام الصحيحة الموجبة المساوية أو الأصغر من س، ما عدا الرقم الصفر. يُمَثَّل العاملي رياضيًا بوضع علامة تعجب بجانب الرقم.
إن لم تفهم التعريف فستفهمه بالأمثلة التالية:
4!
5!
6!
7!
8!
وتُقرأ المسألة الأولى: عاملي الأربعة. حلها سهل، بما أن التعريف يقول إن عاملي 4 يساوي ضرب كل الأرقام الصحيحة الموجبة المساوية أو الأصغر من 4، ما عدا الصفر.
الإعداد الموجبة الأصغر أو المساوية للعدد 4: 4, 3, 2, 1. إذن سنضرب كل هذه الأرقام لنرى الناتج:
4x3x2x1 = 24
حل المسألة الأولى يساوي 24.
المسألة الثانية الآن، عاملي الخمسة:
5! = 5x4x3x2x1 = 120
الناتج 120. الآن عليك حل بقية المسائل بنفسك، خذ ورقةً وقلمًا وحلها.
وقت التشغيل Running Time

عندما نتكلم عن خوارزمية فعلينا معرفة وقت تشغيلها، الوقت الذي تتطلبه لتعمل. ما الفائدة؟
لاختيار أكفأ خوارزمية!
تعلمنا خوارزمية البحث الثنائي وعرفنا أنها أسرع من خوارزمية البحث الخطي، لكن كم وقت تشغيلها؟ كم ستختصر وقتًا؟
خوارزمية البحث الخطي للبحث عن عنصر في لائحة من مائة عنصر ستخمِّن مائة تخمين في أسوأ حالة. إذا كانت اللائحة مكونة من أربعة ألف مالِ ألفٍ (billion: رقم واحد بجانبه تسعة أرقام: 1,000,000,000) فإنها ستأخذ عدد تخمينات قدرها -في أسوأ حالة- أربعة ألف مالِ ألف.
إذن نستنتج أن عدد التخمينات الأقصى، أي في أسوأ حالة، يساوي نفس حجم اللائحة، وقد وضَّحت ذلك في الدرس السابق، لكن ما لم أقله أن هذا يسمى بالوقت الخطي liner time، ويقصد به أن عدد التخمينات يساوي حجم اللائحة.
خوارزمية البحث الثنائي مختلفة عن خوارزمية البحث الخطي، فاللائحة المكونة من مائة رقم ستأخذ فيها الخوارزمية سبعة تخمينات فقط في أسوأ حالة، أما القائمة المكونة من أربعة ألف مالِ ألف رقم ستأخذ فيها الخوارزمية اثنين وثلاثين محاولة فقط، أليس البون شاسع!
خوارزمية البحث الثنائي تعمل في الوقت الأسيسي (اللوگاريثمي)، ما يعرف بالإنگليزية logarithmic time، أو اختصارًا log time.
توقف للحظة، كيف عرفت أن الناتج يساوي اثنين وثلاثين؟
يحزنني ويغضبني سماع هذا منك، ألم تدرس الدرس الأول جيَّدًا؟!
أتفقنا إننا لو أردنا معرفة أقصى عدد تخمينات أن نستعمل الأسيس logarithm الذي تعلمناه في الدرس السابق:
لو 4,000,000,000 = 32
يُقرَأ: أسيس العدد ألف مالِ ألف للأساس اثنين يساوي اثنين وثلاثين. لا تسألني لماذا الأساس اثنين، فقد ذكرناه في الدرس السابق، وسبق شرحه.
كل مقال يُبنى على الأول، لن تفهم الدرس الثاني دون فهم الدرس الأول، ولن تفهم الدرس الثالث دون فهم الدرس الثاني لأن العلم معرفة تراكمية، وبيان هذا اقتباسٌ أسوقه الآن من كتاب «التفكير العلمي»:
«العِلمُ مَعرِفةٌ تَراكُمِيَّة. ولَفظُ «التَّراكُمِية» هَذا يَصِفُ الطَّرِيقةَ التي يَتطوَّرُ بِها العِلْم، والتي يَعلُو بِها صَرْحُه؛ فالمَعرِفةُ العِلْميةُ أَشْبهُ بالبِناءِ الذي يُشيَّدُ طابَقًا فَوقَ طابَق، معَ فارِقٍ أَساسِيٍّ هُو أنَّ سُكَّانَ هَذا البِناءِ يَنتقِلُونَ دَوْمًا إلَى الطابَقِ الأَعْلى؛ أيْ أنَّهُم كُلَّما شَيَّدوا طابَقًا جَدِيدًا انْتَقلُوا إلَيْه وتَركُوا الطَّوابِقَ السُّفْلى لتَكونَ مُجرَّدَ أَساسٍ يَرتكِزُ عَلَيه البِناء».
تعقيد الوقت ورمز O الكبير
سنَلِجُ الآن إلى تعقيد الوقت time complexity، وسيزداد الأمر إثارة، فتأهب!
تعقيد الوقت يُقدِّر الوقت المستغرق لتنفيذ الخوارزمية. عادةً يقدر تعقيد الوقت بحساب عدد مرات تنفيذ الخوارزمية لا بمقدار الثواني أو الدقائق التي ستستغرقها الخوارزمية، ولذلك لأن لدينا عدة معايير لقياس فعالية الخوارزمية، مثل الوقت وعدد مرات تنفيذها والذاكرة والمساحة.
في تعقيد الوقت لدينا ثلاث حالات:
أفضل حالة best case.
حالة متوسطة average/middle case.
أسوأ حالة worst case.
لكل من الحالات الثلاث رمز خاص، هي على التوالي:
1. Omega Notation | Ω
2. Theta Notation | θ
3. Big O Notation | O
لنفترض أن لدينا لائحة من مائة عنصر، لو كان العنصر الذي نبحث عنه أول عنصر فهذه أفضل حالة، وإن كان العنصر الذي نبحث عنه في الوسط فإن هذه الحالة المتوسطة، ولو كان العنصر في آخر اللائحة فهذه أسوأ حالة.
في بعض المراجع تختلف أسماء تلك الحالات، فتسمى بالترتيب:
1. Lower bound.
2. Tight bound.
3. Upper bound.
كل شرحنا سيكون لأسوأ حالة، أما الحالة المتوسطة فإننا سنقابلها في الفصل الرابع من الكتاب. لِمَ أسوأ حالة؟
لأنك مبرمج، وهذا عملك، عليك أن تعلم كيف سيعمل الرِمَاز في أسوأ حالة له، فتحسنه ليكون قريبًا من أفضل حالة. فشعار المبرمج: العمل للأسوأ والتخطيط للأفضل (work for worst and plan for best).
ولحساب تعقيد الوقت في أسوأ حالة فإن لدينا شيء يسمى رمز O الكبير (بالإنگليزية: Big O Notation)، نستخدمه لحساب تعقيد الزمن للخوارزمية في أسوأ حالة. لا ريب أنك ستستخدم خوارزميات كتبها بعض الأنام، فمن المهم أن تفهم أي خوارزمية أسرع وأيها أبطأ.
سنرى استعمالها الآن، فتحلى بالصبر، فقد حان وقت المثال، فهذا المثال التالي سيريك استعمالها وسيريك كيف أن وقت تشغيل الخوارزميات ينمو في معدلات مختلفة.
المثال
عبود، مبرمج يعمل لدى وكالة الفضاء الدولية ناسا NASA، طُلِبَ منه كتابة خوارزمية تعمل عند بدء تشغيل الصاروخ، ليحدد المنطقة التي سيهبط فيها الصاروخ على القمر.

عبود متابع حديث لموقعنا، وقد قرأ المقال السابق وتعلم خوارزميتي البحث الثنائي والخطي، فرغب في استعمال إحداهما لتنفيذ المهمة المناطة به.
يريد عبود أن تكون الخوارزمية سريعة وصحيحة، سريعة لأنه يمتلك عشر ثوانٍ قبل انطلاق الصاروخ، وصحيحة ليحدد موقع هبوطه بدقة لكيلا يُطرَدُ!
فكر عبود أن خوارزمية البحث الثنائي أسرع، لكن سرعان ما وسوس له الشيطان بأن خوارزمية البحث الخطي أسهل للكتابة فلن تتسبب في أخطاء في الرِمَاز code. وعبود لا يرغب بأي أخطاء في رِمَازه.
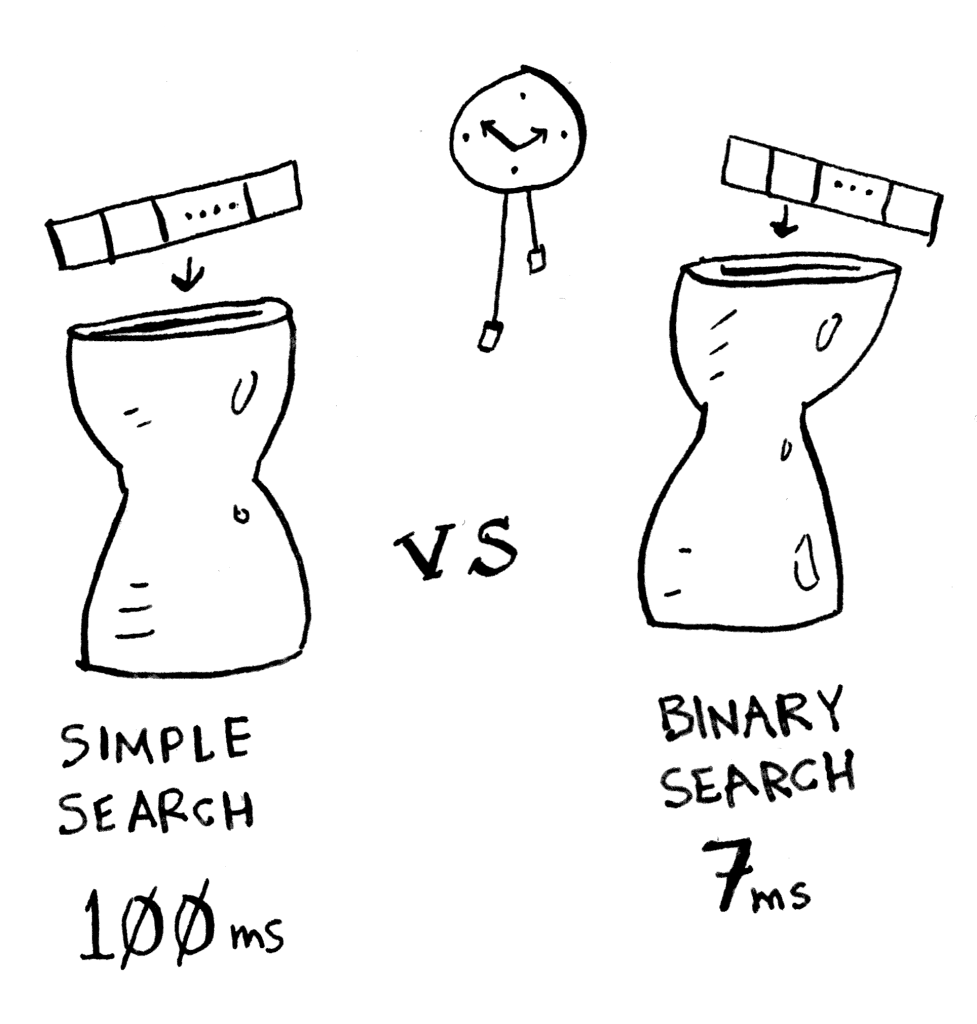
احتار عبود أي الخوارزمين سيستعمل، لذا سيختبر مقدار الوقت المستهلك للخوارزميتين بلائحة مكونة من مائة عنصر.
وجدت عبود أن كل عملية تحقق لعنصر واحد في اللائحة تستغرق وقتًا قدره واحد مئلاف ثانية (one millisecond). بما أن حجم اللائحة مائة عنصر فإن خوارزمية البحث الخطي ستستغرق مائة مئلاف ثانية (100*1=100). أما خوارزمية البحث الثنائي فستستغرق سبعين مئلاف ثانية، لأنها ستأخذ سبع خطوات فقط، فسبعة في واحد يساوي سبعة (7*1=7).
اللائحة المكونة من مائة عنصر كان مجرد اختبار يجريه عبود للخوارزميتين، فإن حجم اللائحة الحقيقي سيكون ضخمًا، مثل ألف مالِ ألف عنصر (1,000,000,000)، فكم ستستغرق كِلا الخوارزميتين، خوازرمية البحث الثنائي والخطي؟
حاول الإجابة على السؤال قبل مواصلة القراءة…
ذهب عبود لاختبار خوارزمية البحث الثنائي بلائحة عدد عناصرها ألف مالِ ألف عنصر، وقد استغرقتِ الخوارزمية اثنين وثلاثين مئلاف ثانية، بحسب المعادلة الأسيسية (الگوارثمية) التالية:
لو (1000000000) = 32
فكر عبود قائلًا: يا لها من خوارزمية سريعة، أنها أسرع بخمس عشرة مرة من خوارزمية البحث الخطي، لأن خوارزمية البحث الخطي ستستغرق مائة مئلاف ثانية لمائة عنصر، أما خوارزمية البحث الثنائي فستستغرق سبعة مئلاف ثانية لمائة عنصر. إذن فإن 15×30 يساوي 450 مئلاف ثانية.
اتخذ عبود قراره واتبع وسوسة الشيطان واستخدم خوازرمية البحث الخطي، فأربعمائة وخمسين مئلاف ثانية مقدار هيَّن جدًا فلم يصل إلى ثانية واحدة أصلًا، وسيكتب الخوارزمية بسهولة جدًا ويتخلص من هم وجود أخطاء في برنامجه.
هل اختيار عبود صائب؟
انتهى المثال، وإجابة السؤال: لا، بل ارتكب خطأ جسيمًا، فإن خوارزمية البحث الخطي مع عدد مدخلات (حجم لائحة) مقداره ألف مالِ ألف رقم سيكون الوقت المستغرق ألف مالِ ألف مئلاف ثانية، أي ما يعادل أحد عشر يومًا!!
معدل نمو الخوارزميات يختلف اختلافًا بيَّنًا.
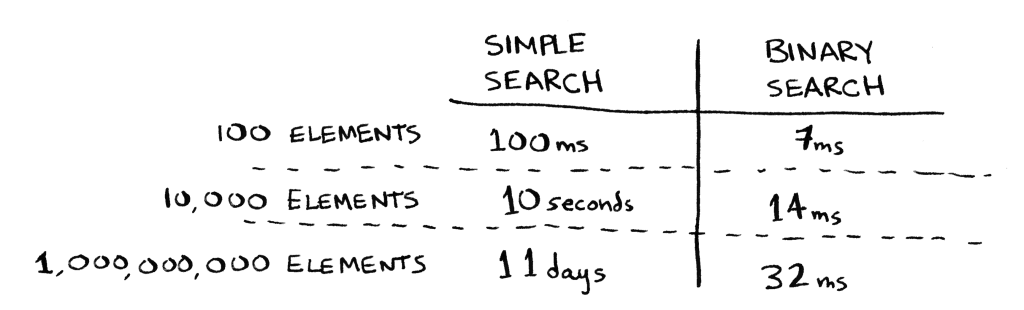
بازدياد عدد العناصر فإن خوارزمية البحث الثنائي ستستغرق وقتًا أقل بكثير، أما خوازرمية البحث الخطي فستستغرق وقتًا أطول.
كلما ازدادت عدد المدخلات ازدادت سرعة خوارزمية البحث الثنائي، أما خوارزمية البحث الخطي فيحدث العكس تمامًا.
توهَّم عبود أن خوارزمية البحث الثنائي أسرع بخمس عشرة مرة، والحقيقة أنها أسرع بثلاثةٍ وثلاثين ألف مالِ ألف مرة (33 billion).
خطأ عبود يريك أن وقت تشغيل الخوارزمية يزداد بزيادة عدد المدخلات (حجم اللائحة)، وهنا يأتي دور رمز O الكبير لمعرفة وقت تشغيلها.
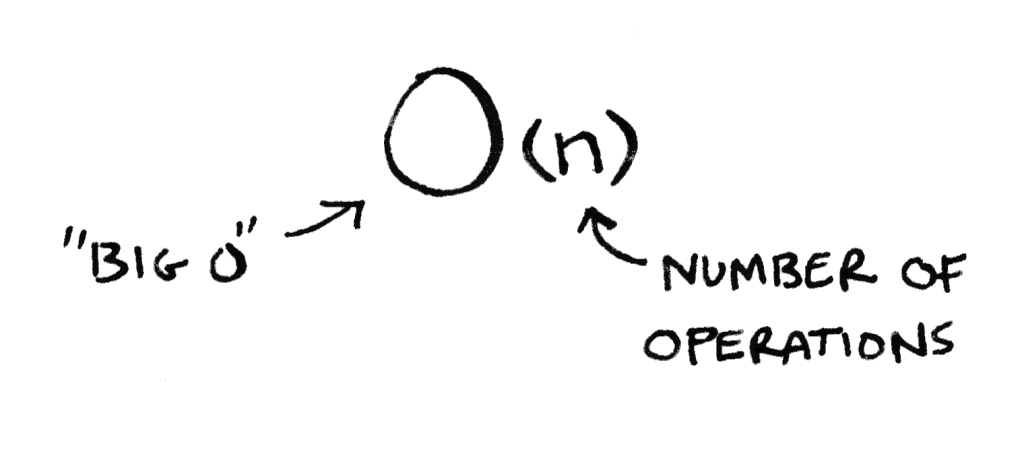
يظهر لك رمز O الكبير سرعة الخوارزمية. لنفترض أن لديك لائحة من س رقم، وحرف س متغير قد يكون أي رقم، فهو المجهول في الرياضيات. ألا تتذكر السين والصاد في حصة الرياضيات؟
خوارزمية البحث الخطي ستتحقق من كل عنصر في اللائحة لذا فإنها ستحتاج إلى س محاولة أو عملية تحقق، وحرف س يساوي حجم اللائحة. وقت التشغيل في رمز O الكبير سيُكتَبُ هكذا:
O(س)
خوازرمية البحث الثنائي تحتاج إلى لو (س) عملية تحقق. فما رمز O الكبير لها؟
أحسنت، هو بالصيغة الإنگليزية:
O(log n)
حيث n هي س المجهول، فبعد حل المعادلة الموجودة بين القوسين (log n) سيظهر مرات تشغيل الخوارزمية.
الصيغة باللعربية:
O(لو س)
ماذا حل بعبود؟
ضربوه ضربًا مبرحًا وطردوه من الوظيفة، وها هو ذا عاطل عن العمل يقضي جل وقته في اللهو واللعب. إن كنت لا ترغب بنفس مصير عبود فركز في دروسنا وذاكرها وافهمها فهمًا.
توقف للحظة، أين الثواني؟
سأصدمك، لا توجد ثوانٍ، رمز O الكبير لا يخبرك بسرعة الخوارزمية بالثواني. وكما قلت لك في بداية الفقرة، إن لدينا معايير مختلفة لحساب كفاءة وفاعلية الخوارزمية، من ضمنها الوقت وعدد مرات تشغيل الخوارزمية، وغيرهما…
والوقت ليس معيارًا ثابتًا، فإن الخوارزمية السريعة على حاسوبي قد تكون بطيئة على حاسوبك لاختلاف العتاد hardware وأشياء أخرى، فإن السرعة تتأثر بعوامل عديدة.
رمز O الكبير يظهر عدد العمليات للخوارزمية، مرات تنفيذ الخوارزمية، وهذا سيخبرك أي خوازرمية أسرع، فالمشهور أن نحسب وقت تشغيل الخوارزمية بعدد مرات تنفيذها أو بعدد مدخلاتها لا الوقت. لذا فإن لفظة “وقت” قد تربك المتعلم لأنه لا يُقصَدُ بها الوقت أصلًا، وأقترح أن تسميها عدد مرات تنفيذ الخوارزمية، أو سرعة الخوارزمية، وهذا سيظهر لك باستخدام رمز O الكبير.
مثال لاستعمال رمز O الكبير
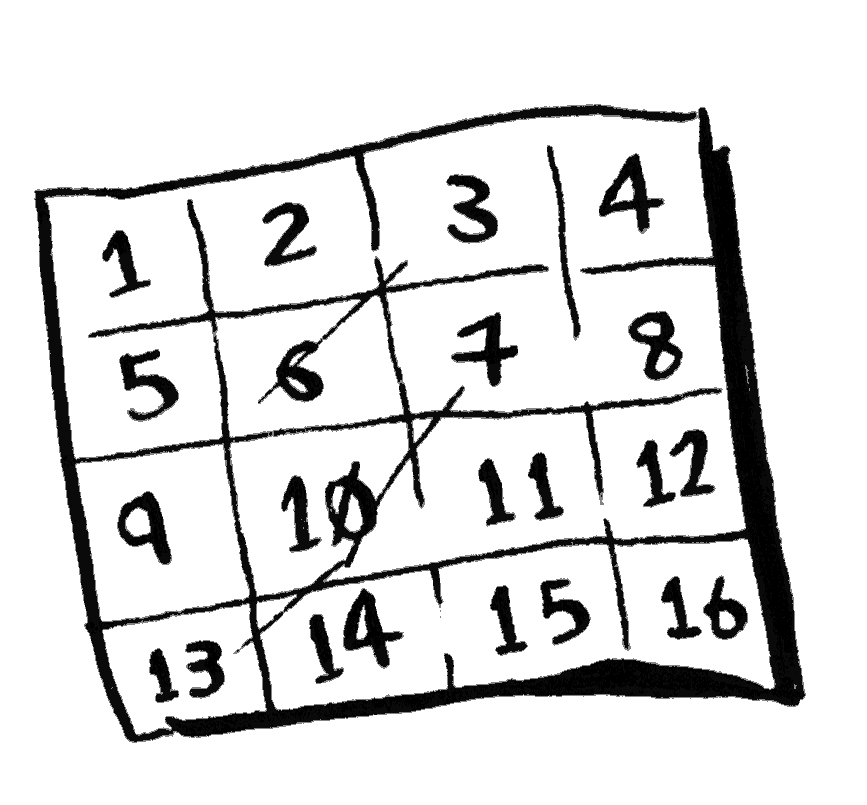
هذا مثال عملي، يتطلب ورقةً وقلمًا لرسم ستة عشر مربعًا على الورقة. سنحلها بخوارزميتين مختلفين لنرى الأسرع ونستخدم رمز O الكبير.
الخوارزمية الأولى
هذه طريقة لرسم ستة عشر مربعًا، في كل مرة نرسم مربعًا واحدًا. تذكر أن رمز O الكبير يحسب لك عدد العمليات التي تجريها الخوارزمية أو عدد مرات تنفيذها. خوارزميتنا هذه ترسم مربعًا في كل مرة، أي في كل عملية.
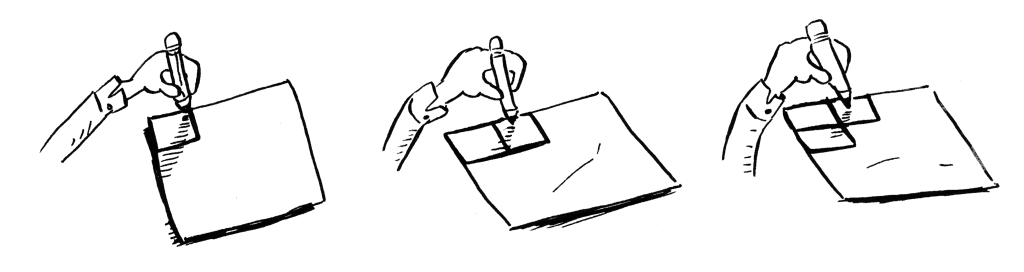
كم تحتاج عمليات لرسم ستة عشر مربعًا؟
ست عشرة خطوة لرسم ستة عشر مربعًا. ما وقت تشغيل هذه الخوارزمية؟
أتفقنا أن رمز O الكبير لمعرفة وقت تشغيل الخوارزمية، وعرفنا كيف نكتبه، فحل السؤال بنفسك قبل المواصلة!
الخوارزمية الثانية
عوضًا عن رسم مربع في كل مرة بالقلم اِطوِ الورقة!
لنطوي الورقة!
في طيَّك للورقة فإنها تُعدُّ خطوة واحدة، وبهذه الخطوة رسمنا مربعين اثنين!
اِطوِ الورقة مرة ومرتين وثلاث.
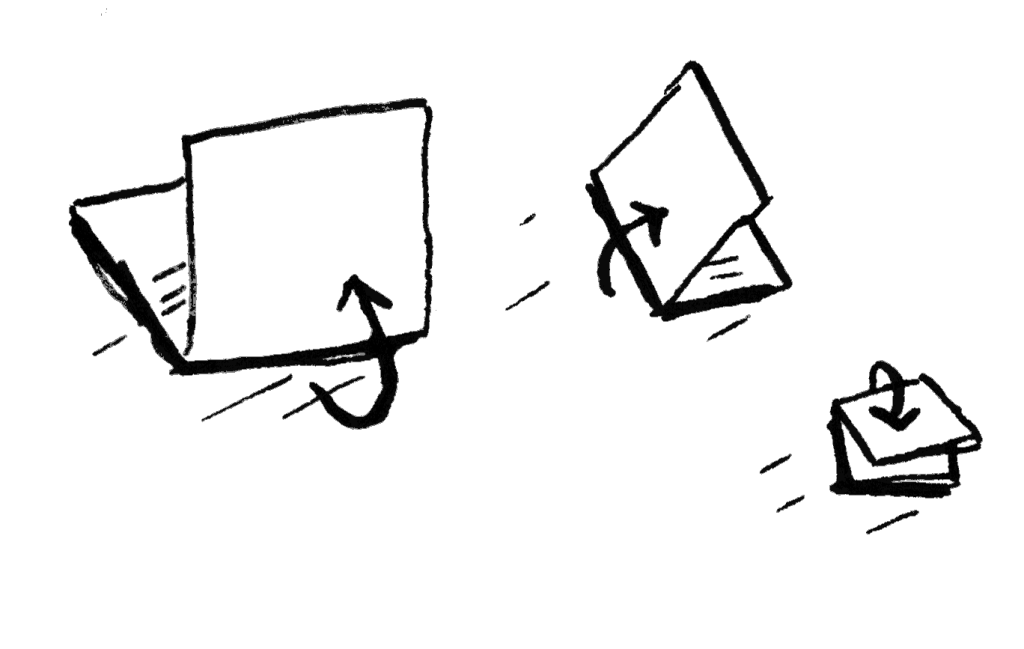
افتح الورقة الآن، سترى شبكة مربعات من ستة عشر مربعًا بأربع مرات لا غير، فقد طوينا الورقة أربع مرات فقط ورسمنا ستة عشر مربعًا. ما وقت تشغيل هذه الخوارزمية؟
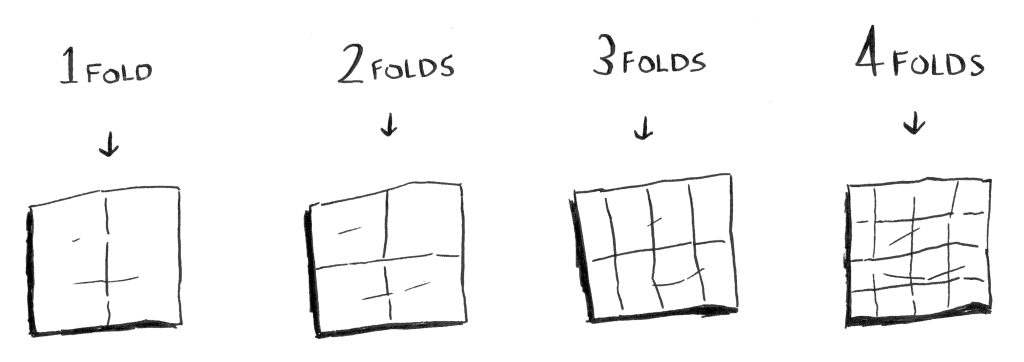
الخوارزمية الأولى وقت تشغيلها:
O(س)
أما وقت تشغيل الخوارزمية الثانية:
O(لو س)
لنحل المسألة بين القوسين. عدد المرات المطلوب رسمها ستة عشر مربعًا، إذن ستكون المعادلة:
لو (16) = 4
أسيس العدد 16 للأساس اثنين (الذي أتفقنا بأننا لن نكتبه) يساوي أربعة، والناتج هو عدد المرات طي الورقة لرسم ستة عشر مربعًا.
أما رمز O الكبير فمعلوم أن خوازرمية البحث الخطي ستستغرق (س)O عملية.
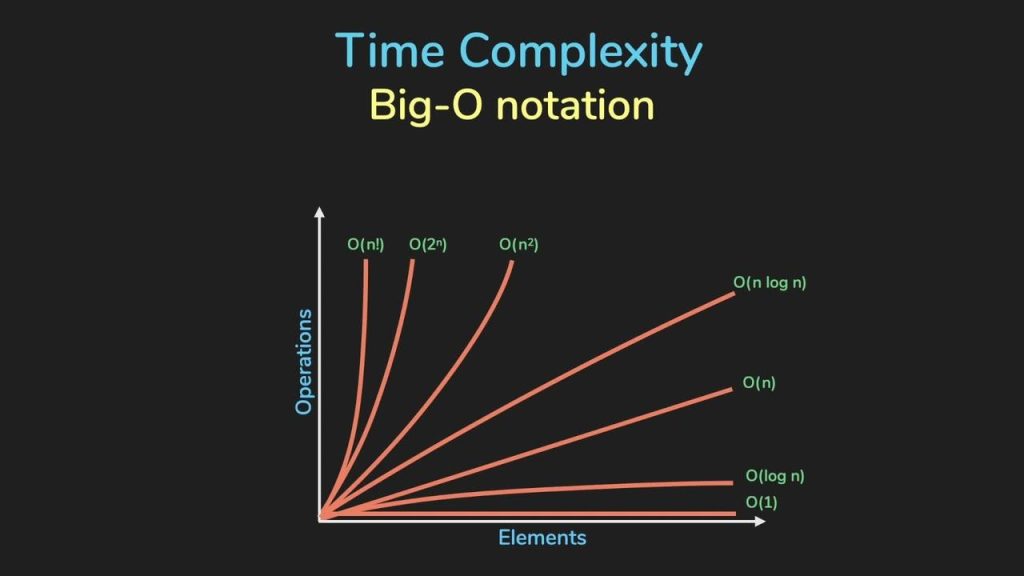
التعقيدات الزمنية الشائعة
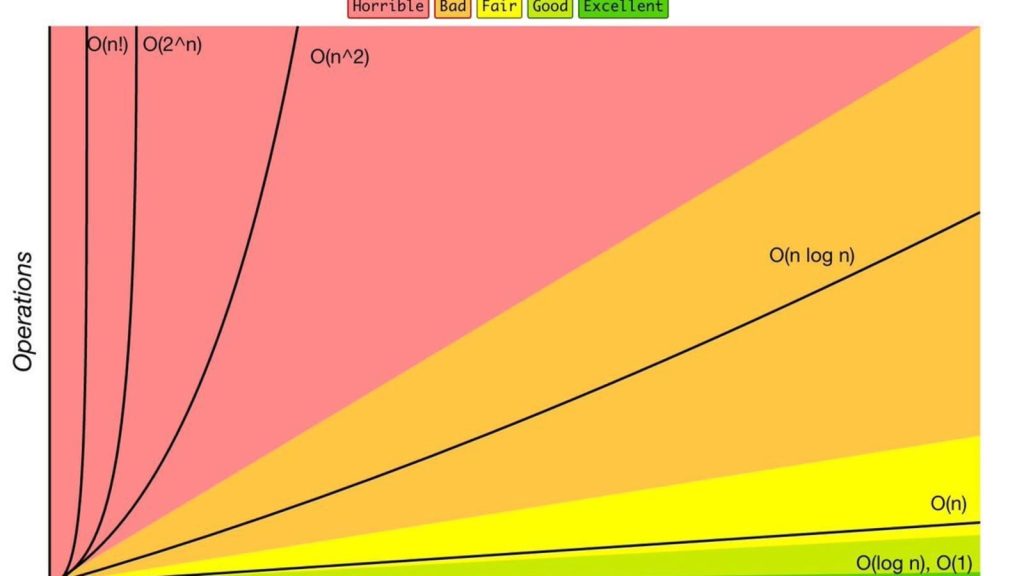
هذه ست تعقيدات زمنية شائعة، مرتبةً من الأفضل حتى الأسوأ. بمعرفة هذه التعقيدات الزمنية سنعرف في أي مستوى تعمل فيه خوارزميتنا، ولو كانت قابلة للتحسين إلى مستوى أفضل حسنَّاها:
1. O(1)
هذه تعد أفضل حالة، لأن الخوارزمية تعمل لمرة واحدة فقط. افترض أنك تبحث عن اسم في دليل الهاتف بخوارزمية البحث الخطي، ولنفترض أن الاسم الذي تبحث عنه هو أحمد، والحمد للّٰه، عثرت عليه في أول محاولة، وهكذا لن تبحث في كل دليل الهاتف، والسؤال: هل ستستغرق الخوارزمية (س)O؟ أم أنها ستستغرق (1)O لأنك عثرت فيه في أول محاولة؟
تستغرق الخوارزمية (1)O. إن كانت خوارزميتك في هذا المستوى فإنه رائعة!
2. (لو س)O
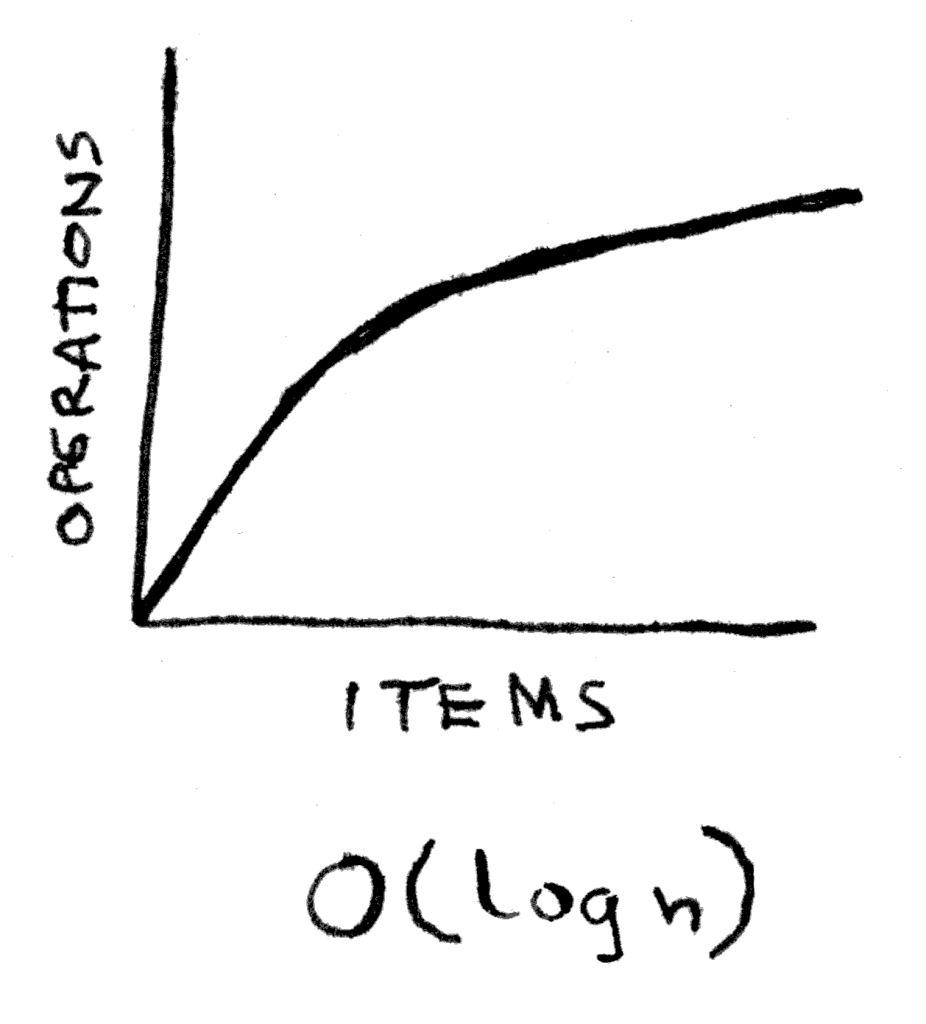
تُعدُّ الخوارزميات في هذا المستوى من أحسن وأسرع الحلول. يُعرف هذا المستوى بالوقت الأسيسي. خوارزمية البحث الثنائي تعمل في الوقت الأسيسي (اللوگاريثمي)، ما يعرف بالإنگليزية logarithmic time، أو اختصارًا log time.
3. (س)O
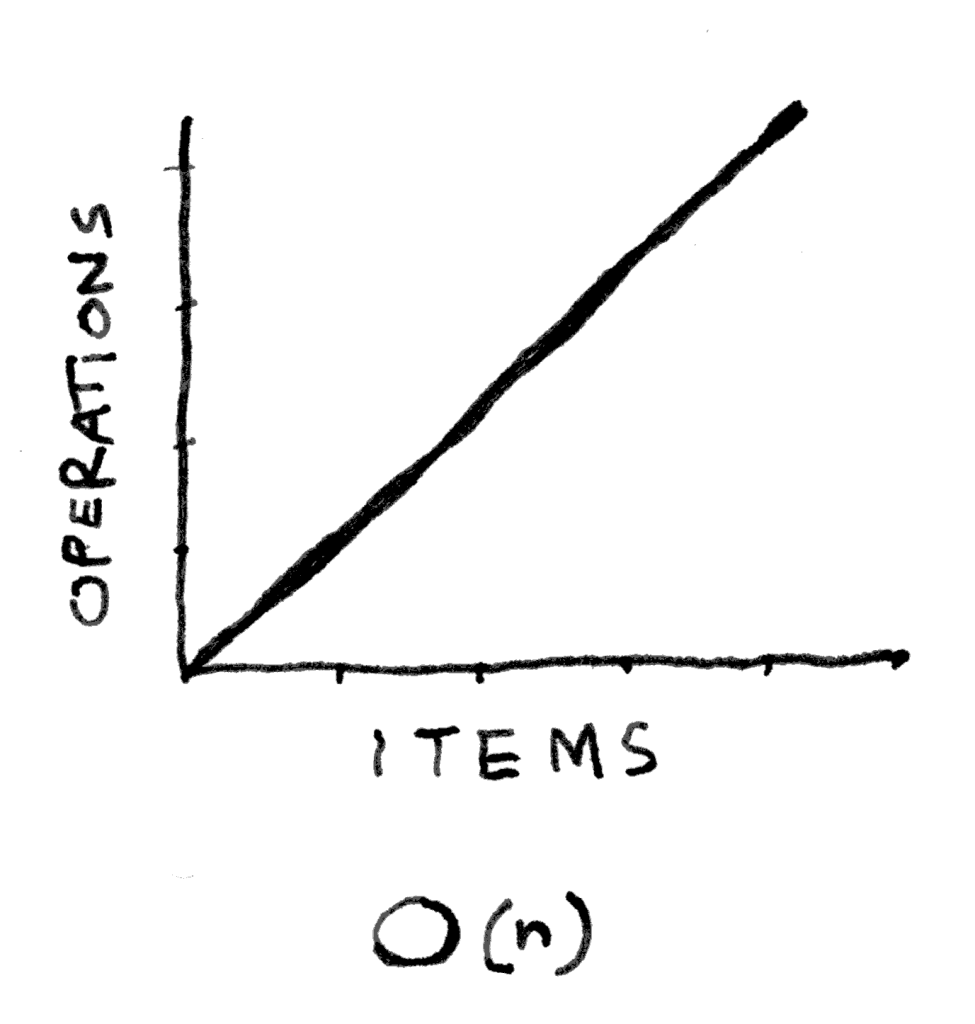
يُعرف هذا المستوى بالوقت الخطي liner time. قد تتساءل لماذا اسمه الوقت الخطي ولماذا خوارزمية البحث الخطي اسمها البحث الخطي؟
لأن الخوارزمية تمر على العناصر خطيًّا، واحدًا تلو الآخر، حتى تنتهي من كل العناصر، كأنها في خطٍ مستقيم. هذا كفيل لتعرف لماذا سُميَّ الوقت الخطي خطيًّا: لأنه يزداد بمقدار خطوة في كل مرة.
الخوارزميات في هذا المستوى لا بأس بها.
4. (س لو س)O
سنستخدمه عند الحديث عن خوارزمية quicksort، في الفصل الرابع.
5. (س²)O
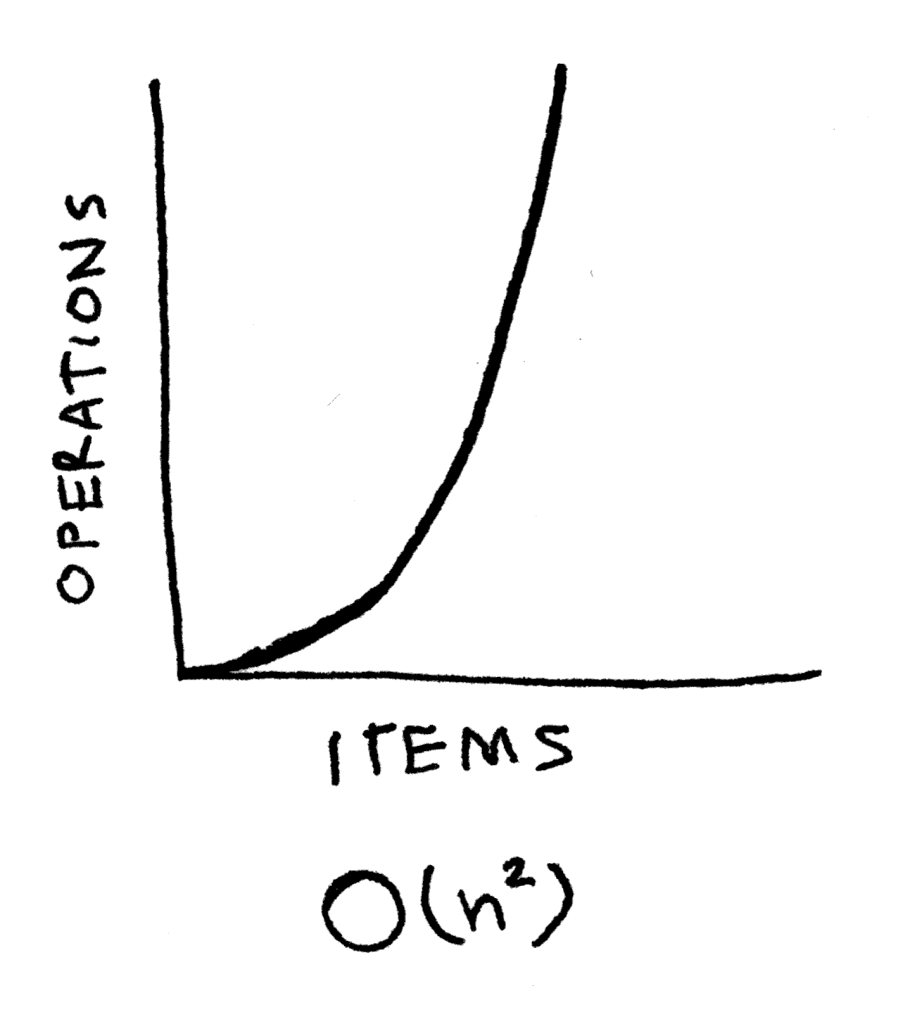
الخوارزميات في هذا المستوى بطيئة، وسنستخدم في الفصل الثاني لخوارزمية selection sort، وقد أوشكنا على الإنتهاء من الفصل الحالي.
6. (!س)O
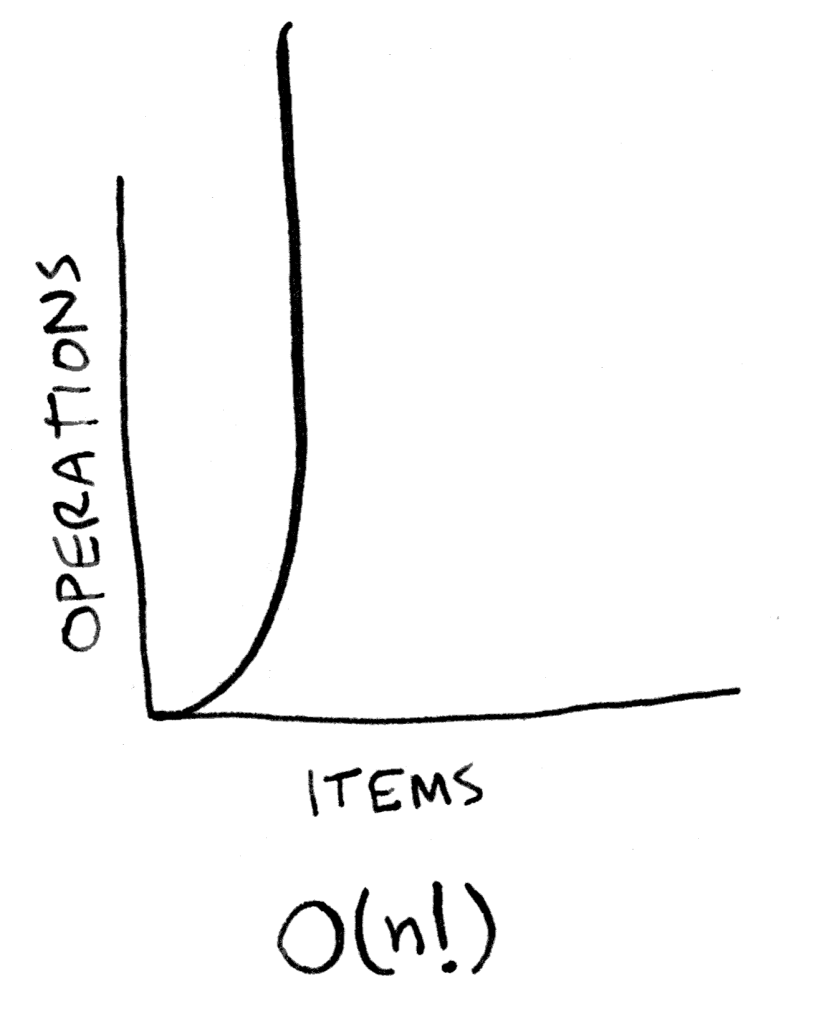
تذكر الآن ما تعلمناه في بداية الدرس، العاملي!
الخوارزميات في هذا المستوى، عاملي س، خوارزميات كارثية بل مرعبة وقد تحتاج إلى آلاف مؤلفة من السنين باستخدام أقوى الحواسيب.
في هذا المستوى سندرس مشكلة البائع المتجول التي ستكون ختام الفصل الأول، وهي المقالة الآتية بعد مقال اليوم. فتابع الموقع أولًا بأول.
عندنا تعقيدات زمنية أخرى مختلفة عن التي ذكرناها، ولكن نكتفي بما ذكرنا وسنعود لرمز O الكبير في الفصل الرابع فلا تقلق.
لنرى تطبيقًا للتعقيدات الزمنية السابقة، وما زلنا في مثالنا السابق، رسم ستة عشر مربعًا.
افترض أنك ترغب برسم ستة عشر مربعًا، ولديك خمس خوارزميات لرسمه، وفي كل عملية فإنها ستأخذ مائة مئلاف ثانية.
إذا استخدمت الخوارزمية الأولى فإن تعقيد الوقت لها هو (لو س)O لرسم ستة عشر مربعًا، أي أنها ستأخذ أربعمائة مئلاف ثانية (لأن لو 16 = 4).
ماذا لو كنت تود رسم 1024 مربعًا؟
ستأخذ الخوارزمية عشر عمليات، لأن لو 1024 = 10، وقد افترضنا سابقًا أن العملية تستغرق مائة مئلاف ثانية، إذن فإن ألف مئلاف ثانية يساوي ثانية واحدة، أي أنك ستستغرق ثانية واحدة لرسم 1024 مربعًا.
خوازرمية البحث الخطي أبطأ، فتعقيد الوقت لها هو (س)O. لرسم ستة عشر مربعًا فإن تعقيد وقتها سيكون ثانية وستة مئلاف ثانية، لأن (16)O هو 16، أي 16 عملية، وقد أتفقنا أن كل عملية تأخذ مائة مئلاف ثانية.
أما لرسم 1024 مربعًا، سيكون تعقيد الوقت لها 1024 عملية. فكم الوقت المستغرق؟
حله قبل المواصلة…
هذه صورة لبقية الخوارزميات مع كل التعقيدات الزمنية لكل خوازرمية:
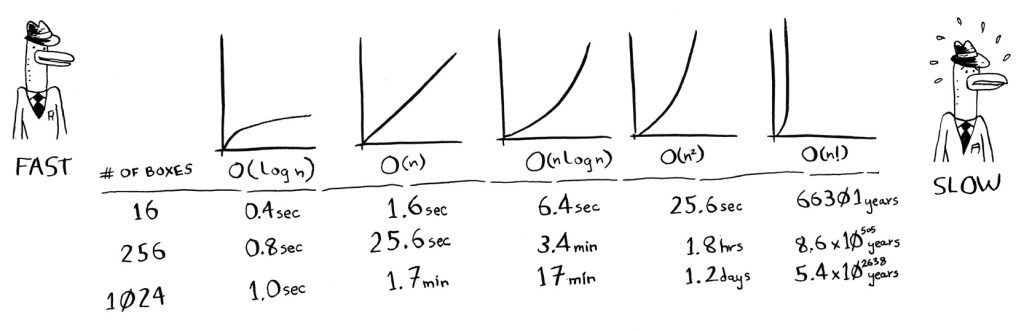
وكما ترى كلما كانت الخوارزمية في مستوى أعلى كلما كان الوقت المستغرق هائلًا، ففي مستوى عاملي س، فإن الخوارزمية ستستغرق 66301 عامًا لرسم ستة عشر مربعًا!
الخلاصة
1. الخوارزميات لا تُقاس بالثواني عادةً، ويزداد معدل نمو الخوارزمية بحسب المدخلات.
2. يعبر التعقيد الزمني للخوارزمية برمز O الكبير (Big O Notation).
3. الخوارزميات ذات تعقيد الوقت (لو س)O أسرع من الخوارزميات ذات تعقيد الوقت (س)O، وتزداد سرعة الخوارزميات ذات تعقيد الوقت (لو س)O كلما زادت المدخلات، مثلًا تكون الخوارزمية أسرع كلما زاد حجم اللائحة…
حل التمارين
وفي هذه الفقرة نحل تمارين الدرس السابق إن وُجِدَت.
حل التمرين الأول: سبع خطوات، لأن لو2(128) يساوي 7.
حل التمرين الثاني: ثمان خطوات فقط!
الخاتمة
لن تكون هنا نهايتنا بل بدايتنا لسلسلة متكاملة وشاملة عن الخوارزميات، وسأشرح الكتاب كاملًا، وستغنيك المقالات المنشورة عنه عن قراءته.
وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.