السلام عليكم ورحمة الله تعالى وبركاته، هذا الدرس الأخير من الفصل الأول من كتاب «استيعاب الخوارزميات» الذي بدأناه. لفهم ما سنقوله اليوم لا بد أن تقرأ الدرس السابق، الدرس الثاني من كتاب استيعاب الخوارزميات المعنون «تعقيد الوقت ورمز O الكبير».
سنرى اليوم عبود بعد طرده من عمله وهو يعمل بائعًا متجولًا!
قرأتَ المقال السابق وتساءلتَ، عليَّ الامتناع منعًا باتًا من استعمال أو إنشاء خوازرمية رمز O الكبير الخاص بها عاملي س، (س!)O، أي أن تعقيدها الزمني عاملي س. لكني سأريك اليوم مسألة مشهورة تعمل في هذا المستوى المروَّع!
مسألة البائع المتجول
مسألة البائع المتجول Travelling Salesman Problem: بائع متجول اسمه عبود، سيزور عددًا من المدن بأقصر طريق ممكن، كل مدينة سيزورها مرة واحدة فقط، يبدأ رحلته من مدينة محددة، لنفترض أنها مسقط رأسه، وفي النهاية يعود إليها.
التحدي أن يقلل المسافة المقطوعة ليقلل تكلفة السفر من مدينة إلى أخرى، لتوفير الوقود والمال. لا يغرنَّك سهولة شرحها فحلها شديد الصعوبة، بل شبه مستحيل!
مسألة البائع المتجول Travelling Salesman Problem، اختصارًا TSP، من أشهر المسائل في علم الحاسوب. أذكياء القوم يقولون بأنه يستحيل حلها، فقد قضى علماء الرياضيات والحاسوب عقودًا يسعون إلى حلها!
تطبيقات حقيقية
حلها بفعَّالية سيوفر الآلاف والآلاف من الأموال في مختلف القطاعات.
لهذا المسألة تطبيقات كثيرة، فحلها سيوفر آلاف مؤلفة من الأموال، ومن هذه التطبيقات:
1. خدمات التوصيل والنقل
2. تصميم الشبكات
3. توصيل الدارات الكهربائية
4. تسلسل الحمض النووي
مثال تطبيقي
صاحبنا المنحوس عبود أصبح بائعًا متجولًا بعد طرده من وكالة الفضاء الدولية ناسا NASA وأبراحه ضربًا.

عليه زيارة خمس مدن: مارين Marin وسان فرانسيسكو San Francisco وبالو آلتو Palo Alto وبيركلي Berkeley وفريمونت Fremont.
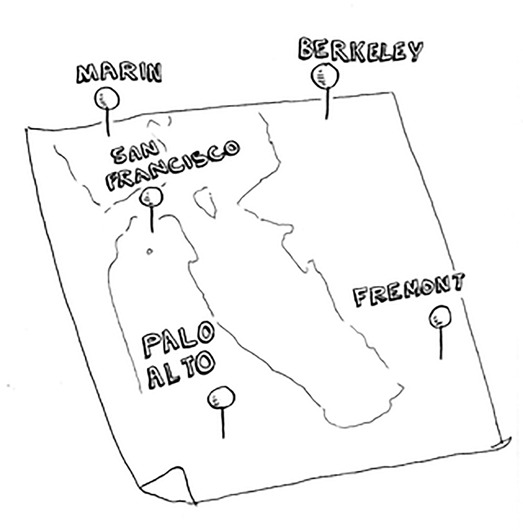
يريد عبود زيارة الخمس المدن بأقصر مسافة. إحدى الطرائق لفعل ذلك مقارنة كل طريق محتمل أن يسلكه، أي أن نستعمل خوارزمية البحث الخطي (كما تقدم شرحها في المقالات السابقة)، فيجمع المسافة الكلية ويختار المسار الأقصر.
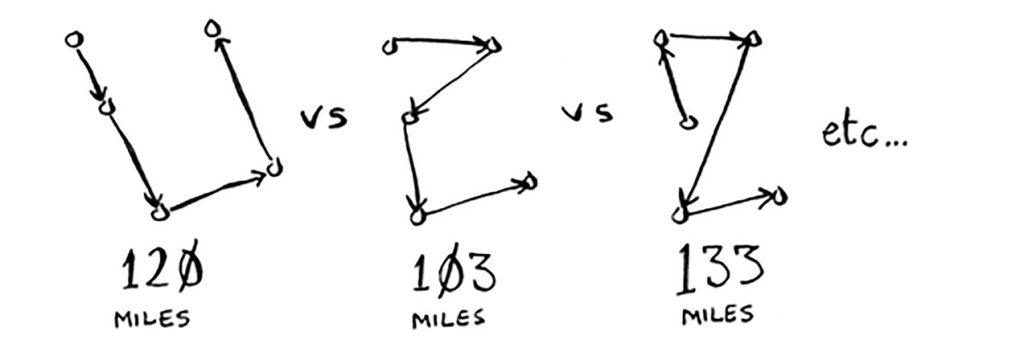
لزيارة خمس مدن فإن الاحتمالات الممكنة ١٢٠ احتمالًا، أما لزيارة ست مدن فإن الاحتمالات الممكنة ٧٢٠ احتمالًا، أما لزيارة سبع مدن فإن عدد الاحتمالات ٥٠٤٠ احتمالًا!

فإنها تنمو نموًّا عامليًّا. أتتذكر العاملي في الرياضيات الذي شرحته في المقالة السابقة؟
في بداية الأمر لمدن قليلة، لنقل ثلاث أو أربع مدن، فإنها سهلة الحل، لكن بازدياد عدد المدن فإن عدد الاحتمالات ينموًا نموًّا عامليًّا. أوجد عاملي 5 و6 و7 و8 لتتحقق من ذلك!
إذن فإن لكل س ستكون عدد الاحتمالات عاملي س. إذن فإن رمز O الكبير لها (س!)O.
إن ازداد عدد المدن إلى مائة مدينة فإنه من المستحيل حلها، فقد تفنى البشرية ولم نصل للحل بعد!
إذن فخوارزمية البحث الخطي ليست خيارًا عقلانيًا. أليس على عبود أن يختار خوازرمية أحسن لحلها؟
لا يستطيع حلها، فهذه من المسائل غير المحلولة في علم الحاسوب. لا توجد خوازرمية يمكنها حلها. أذكياء القوم يقولون بأنه يستحيل إنشاء خوارزمية سريعة فعَّالة لها. كل ما نستطيع فعله تقديم حلول تقريبيَّة فقط، سنناقش هذا في الفصل العاشر لأننا نحتاج إلى معلومات أكثر قبل العودة لمسألة البائع المتجول.
نهاية الفصل
هذا الدرس آخر درس من الفصل الأول من الكتاب، وفي المقالات الآتية سنشرع في شرح الفصل الثاني من الكتاب.
متطلبات قراءة الفصل الثاني أن تكون قد درست الفصل الأول وفهمته فهمًا تامًا، فإن الفصل الأول اللبنة الأساسية لفهم بقية الكتاب.
التمارين
ادرس الدرس الثاني لتحل هذه الأسئلة.
أوجد رمز O الكبير لكل من هذه الافتراضات:
1. تبحث عن اسم فرد في دليل الهاتف.
2. تبحث عن رقم شخص في دليل الهاتف (تمليح: ستبحث في الكتاب كله).
3. ترغب بقراءة كل الأرقام في دليل الهاتف.
4. ترغب بقراءة كل الأرقام للأفراد الذين يبدأ اسمهم بالحرف ألف أ A. (أحذرك! هذا صعب جدًا، وينطوي على مفاهيم سنتعرف عليها في الفصل الرابع).
هذه المرة لن أحل هذه الأسئلة في المقالة الآتية.
الخاتمة
ها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.