كتاب استيعاب الخوارزميات -الفصل الرابع، الدرس الأخير- خوارزمية الفرز السريع

السلام عليكم ورحمة الله تعالى وبركاته
سنتعلم اليوم ثاني خوارزمية فرز لنا في الكتاب، وقد كانت أول خوارزمية تعلمناها خوارزمية الفرز بالانتقاء selection sort، وخوارزمية اليوم أسرع من خوارزمية الفرز بالانتقاء!

مقال اليوم متعلق أشدة علاقة بالمقال السابق، مقال فَرِّق تَسُد، ولا مندوحة لك عنه، لأننا سنبني عليه درس اليوم، فإن لم تدرسه فادرسه وثم عد لهذا الدرس، وهذا الدرس الأخير من الفصل الرابع، درس خوارزمية الفرز السريع!

خوارزمية الفرز السريع

خوارزمية الفرز السريع quicksort algorithm خوارزميةُ فرزٍ فعالة وسهلة، ومن أشهر خوارزميات الفرز الحالية، وصفها Hoare عام 1962، تقوم على مبدأ فَرِّق تَسُد divide and conquer، الذي سبق وشرحناه.

عمل الخوارزمية سهل الفهم، ركز معي!
تَبدأ خوارزميةُ الفرز السريع بمسْحِ اللائحةِ المراد فرزها للبحث عن القيمة المتوسِّطة، وهذه القيمة نسميها هاهنا بالمُرتكَز pivot.
ولِمَ نختار قيمة نسميها بالمُرتكَز يا مبعسس؟
ويحك! لا تقاطعني وواصل القراءة!

بعد العثور على تلك القيمة، فإن هذه القيمة (المسماة المرتكَز pivot) تُوضَعُ في نهاية اللائحة.

تُنقَلُ بعدها جميعُ العناصر الموجودة في اللائحة، التي تَقلّ قيمُها عن قيمةِ المرتكَز إلى أحد طرفي اللائحة، وتُنقَلُ العناصرُ التي تزيد قيمُها على قيمةِ المرتكَز إلى الطرف الآخر من اللائحة.

ولهذا حددنا قيمة المُرتكَز، لأننا سنقسم اللائحة إلى قسمين، قسمٌ عناصره أصغر من قيمة المُرتكَز، وقسمٌ عناصره أكبر من قيمة المُرتكَز.

يُعاد فرزُ كلِّ طرفٍ من طرفَي اللائحة بالطريقة ذاتها، حتى الحصول على لائحةٍ نهائية مفروزة كليّا.

سأعيد توضيح الخطوات من جديد، لأنك لو فهمتها فهمت الخوارزمية!
الخطوة الأولى: لدينا لائحة، لنسميها اللائحة الأم أو الأساسية، وثم من هذه اللائحة نأخذ عنصرًا ليكون المُرتكَز pivot.
الخطوة الثانية: بحسب قيمة المُرتكَز سنقسم اللائحة إلى قسمين، قسمٌ عناصره أصغر من قيمة المُرتكَز، وهذه اللائحة الأولى، وقسمٌ عناصره أكبر من قيمة المُرتكَز، وهذه اللائحة الثانية.

الخطوة الثالثة: سنعيد تكرار الخطوة الأولى على اللائحة الأولى التي عناصرها أصغر من قيمة المُرتكَز، وعلى اللائحة الثانية التي عدد عناصرها أكبر من قيمة المُرتكَز.

هذه ثلاث خطوات ستتكرر في الخوارزمية، في الخطوة الثالثة ستظهر قيمة مُرتكَز للائحة الأولى، لأنها لائحة جديد ولا بد من مُتكَزٍ جديد خاص بها، وبهذا تتفرع اللائحة الأولى إلى قسمين، قسم عدد عناصره أصغر من قيمة المُرتكَز الخاص بهذه اللائحة الفرعية، وقسم عدد عناصره أكبر من قيمة المُرتكَز.

وبالمثل فإن اللائحة الثانية التي عدد عناصرها أكبر من قيمة المُرتكَز ستتفرع إلى لائحتين فرعيتين كما حدث مع اللائحة الأولى، وسيكون لها قيمة مُرتكَزٍ أيضًا فأنى لنا تقسيم اللائحة دون قيمة مُرتكز ترتكز عليها في التقسيم؟ وكل لائحة فرعية ستتفرع بدورها إلى لائحتين فرعيتين وهكذا حتى نصل إلى نقطة أن اللائحة مفروزة كاملًا.

لا تخف إن تُهتَ ولم تفهم، فبهذا المثال العملي سنستعمل خوارزمية الفرز السريع وستفهم بلا ريب!

المثال العملي

لنبدأ المثال بسؤال: ما أصغر صفيفة array نقدر فيها على استعمال الخوارزمية (خوارزمية الفرز السريع) لفرزها؟
فكر قليلا وأكمل القراءة…
بعض الصفيفات arrays لا تُفرَز، مثل الصفيفة الفارغة أو الصفيفة ذات العنصر الواحد، بل تُرجَع الصفيفة كما هي.

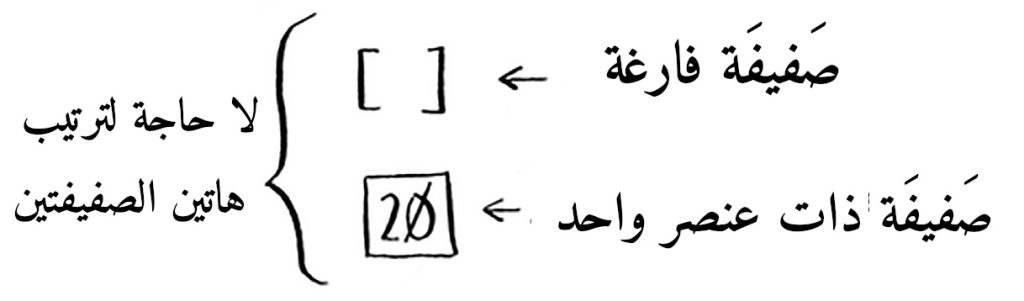
لنُكبَّر الصفيفة ذات العنصر الواحد ونضيف لها عنصرًا جديدًا، صفيفة من عنصرين، كيف سترتبها؟
انظر الصورة:

ماذا عن صفيفة من ثلاثة عنصرين [٣٣،١٥،١٠]؟ كيف سترتبها؟

لا تنس أننا نطبق مفهوم فَرِّق تَسُد، فيتوجب أن تقسم الصفيفة إلى أجزاء أصغر وهكذا… حتى تصل إلى جزء التوقف base case. لكن ما هو جزء التوقف؟

هو أن تكون الصفيفة ذات عنصر واحد، فنرجعها!
لنستعمل خوارزمية الفرز السريع لترتيب هذه الصفيفة [٣٣،١٥،١٠].
أولا نختار عنصرا في الصفيفة ليكون قيمة المُرتكَز، ولنختار العنصر الأولى ٣٣. سنناقش اختيار المُرتكَز المناسب لاحقًا في هذا الدرس.

ثانيا نجعل العناصر الأصغر من قيمة المُرتكَز في صفيفة، والعناصر الأكبر من قيمة المُرتكَز في صفيفة أخرى.

والخطوة الثانية اسمها التقسيم partitioning، وعندك بعد تطبيق هذه الخطوة:
١. صفيفة عناصرها أصغر من قيمة المُرتكَز
٢. المُرتكَز
٣. صفيفة عناصرها أكبر من قيمة المُرتكَز

 

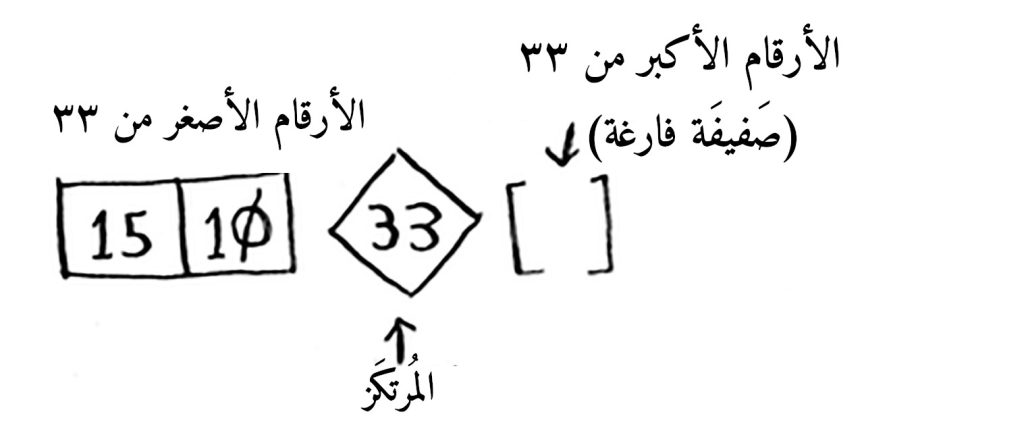
الصفيفتان الفرعيتان غير مفروزتين، قسمنا فحسب، سيكون فرزها سهلا:

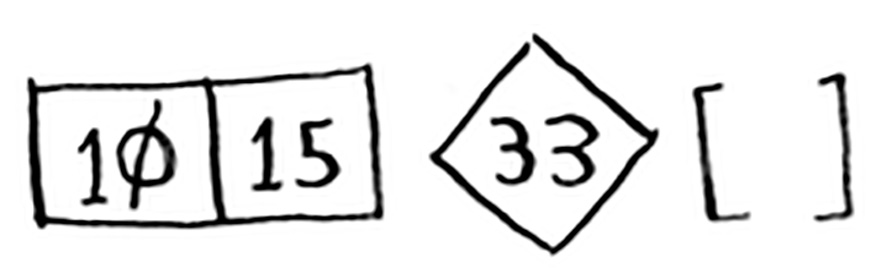
وبما أن الصفيفتين مفروزتين فإننا سنجمع تلك الأجزاء معًا، هكذا: الصفيفة الأولى + المُرتكَز + الصفيفة الثانية. وبجمعها تُفرز الصفيفة كاملًا.

في صفيفتنا السابقة [١٠،١٥] + [٣٠] + [] = [١٠،١٥،٣٣].
قد علمنا كيف نفرز صفيفة من عنصرين، وتعلمنا كيف فرز صفيفة فارغة (عد لبداية الفقرة).

إذا استدعينا خوارزمية الفرز السريع على الصفيفة ذات العنصرين، والصفيفة الفارغة وجمعناها مع المُرتكَز = فُرِزَت الصفيفة!

quicksort([15,10]) + [33] + quicksort([])

> [10,15,33]

ماذا لو كان الصفيفة من أربعة عناصر؟

 

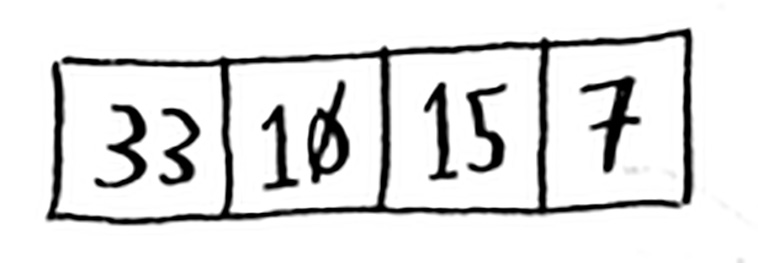
لنختر العنصر الأول ٣٣ ليكون قيمة المُرتكَز مرة أخرى. سنرى صفيفتين، واحدة فارغة، اليمنى، والثانية فيها ثلاثة عناصر.

أنت تعرف مسبقًا كيف نفرز صفيفة من ثلاثة عناصر، استدعي خوارزمية الفرز السريع عَوْدِيًّا recursively.

إذن تستطيع فرز أي صفيفة من أربعة عناصر، وبما أنك تستطيع ترتيبها، فإنك قادر على ترتيب أي صفيفة من خمسة عناصر!
انظر إلى هذه الصفيفة ذات الخمسة عناصر:

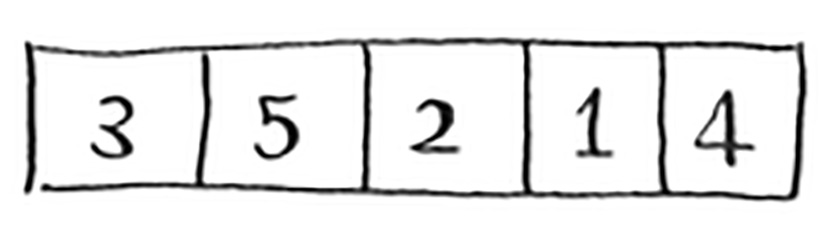
ولنختر العنصر الأول ٣ ليكون قيمة المُرتكَز، ولنستدعِ خوارزمية الفرز السريع على الصفيفات الفرعية sub-arrays:

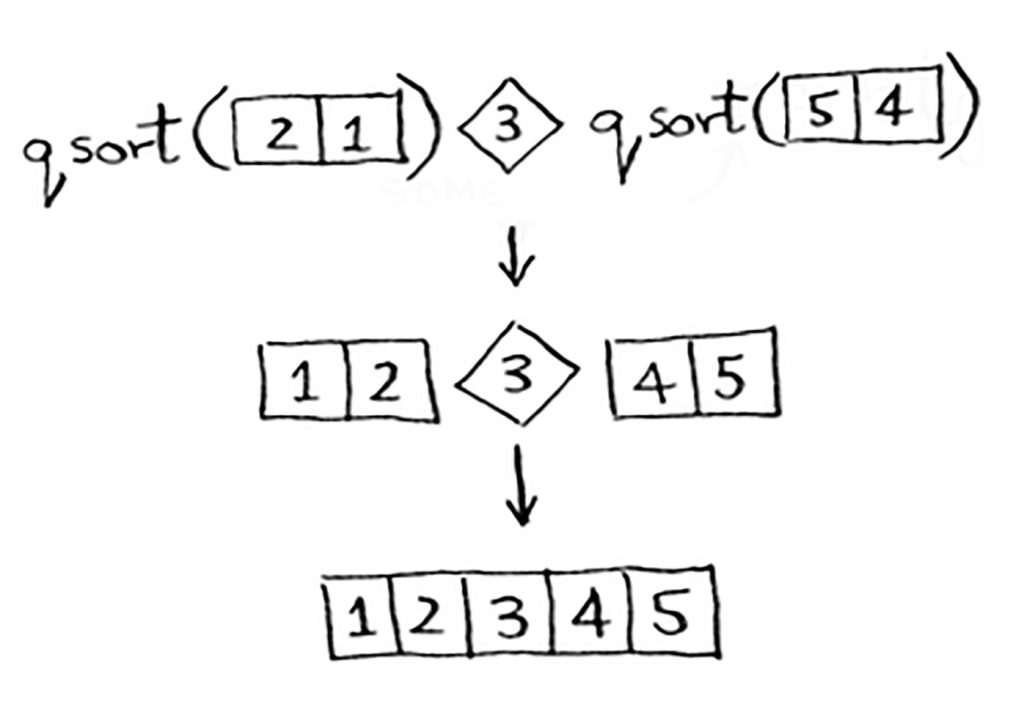
الصفيفات الفرعية فُرِزَت، ثم تستطيع جمع كل الاجزاء لتكون صفيفة واحدة مفروزة.
وما سبق يعمل ولو أخترت العنصر ٥ ليكون قيمة المُرتكَز:

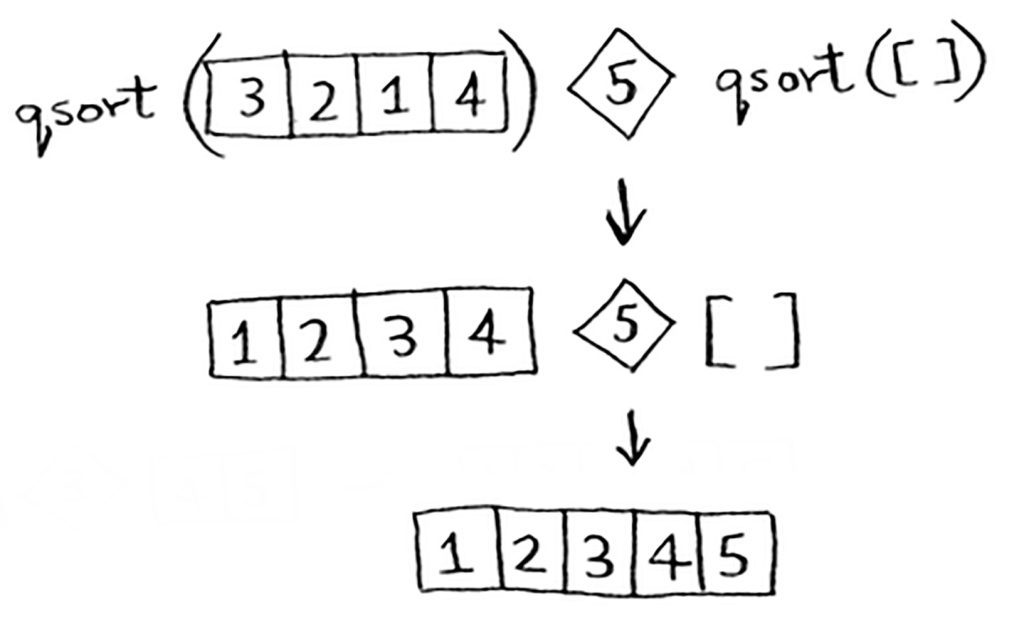
وتستطيع فرز أي صفيفة مهما كان عدد عناصرها بالطريقة السابقة.

هذا رِمَاز خوارزمية الفرز السريع بلغة الثعبان python:

def quicksort(array):
  if len(array) < 2:
    # base case, arrays with 0 or 1 element are already "sorted"
    return array
  else:
    # recursive case
    pivot = array[0]
    # sub-array of all the elements less than the pivot
    less = [i for i in array[1:] if i <= pivot]
    # sub-array of all the elements greater than the pivot
    greater = [i for i in array[1:] if i > pivot]
    return quicksort(less) + [pivot] + quicksort(greater)

print(quicksort([10, 5, 2, 3]))

وهذا رِمَاز خوارزمية الفرز السريع بلغة C:

#include <stdio.h>

// Quick Sort
void quick_sort(int *array, int start, int end) {
	if (start < end) {
		int q = partition(array, start, end);
		quick_sort(array, start, q - 1);
		quick_sort(array, q + 1, end);
	}
}
// Partition by pivot
int partition(int *array, int start, int end) {
	int pivot = array[end];
	int i = start - 1;
	int temp = 0;
	for (int j = start; j < end; j++) {
		if (array[j] <= pivot) {
			i++;
			temp = array[i];
			array[i] = array[j];
			array[j] = temp;
		}
	}
	temp = array[i + 1];
	array[i + 1] = array[end];
	array[end] = temp;

	return i + 1;
}

int main(void) {
	int arr[4] = {10, 5, 2, 3};
	quick_sort(arr, 0, 3);
	// Print result
	for (int i = 0; i < 4; i++) {
		printf("%d ", arr[i]);
	}

	return 0;
}

تعقيد وقت الخوارزميات

ما أسوأ حالة worst case لهذه الخوارزمية؟ ما رمز O الكبير لها؟ ما تعقيد وقتها يا مبعسس!
حسنا، حسنا، لتعلم أن خوارزمية الفرز السريع فريدة لاعتماد سرعتها على اختيارك لقيمة المُرتكَز، فإن كان حَسَنًا ما اخترته كانت سريعة وإلا فالضِّد منه.

ألم كنا نختار العنصر الأول في الصفيفة ليكون قيمة المُرتكَز في كل مرة؟
حسنا، لنجربه مرة أخرى على صفيفة مفروزة، وخوارزمية الفرز السريع لا تتحقق إذا كانت الصفيفة مفروزة أم لا، وهذا هو المثال الأول.
صفيفة من ثمانية عنصر [١،٢،٣،٤،٥،٦،٧،٨]، كما في الصورة:

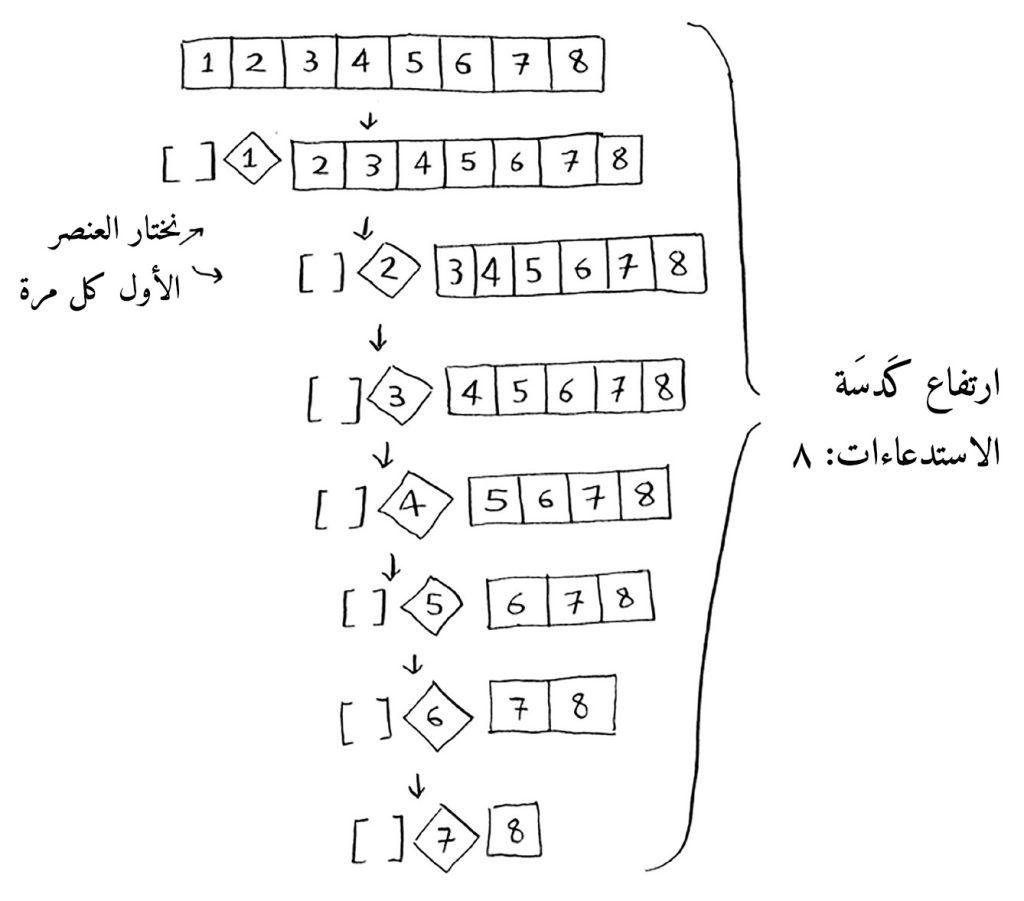
لاحظ كيف تنقسم الصفيفة إلى جزئين كل مرة، وصفيفة فرعية تظل فارغة، وهكذا تكون الكَدسَة stack كبيرة جدًا (راجع الدرس السابق)، أليس سيئا؟

لنجرب اختيار العنصر الأوسط ليكون قيمة المُرتكَز في كل مرة في هذه الصفيفة المفروزة، وهذا المثال الثاني، فانظر هذه المرة إلى ارتفاع الكَدسَة:

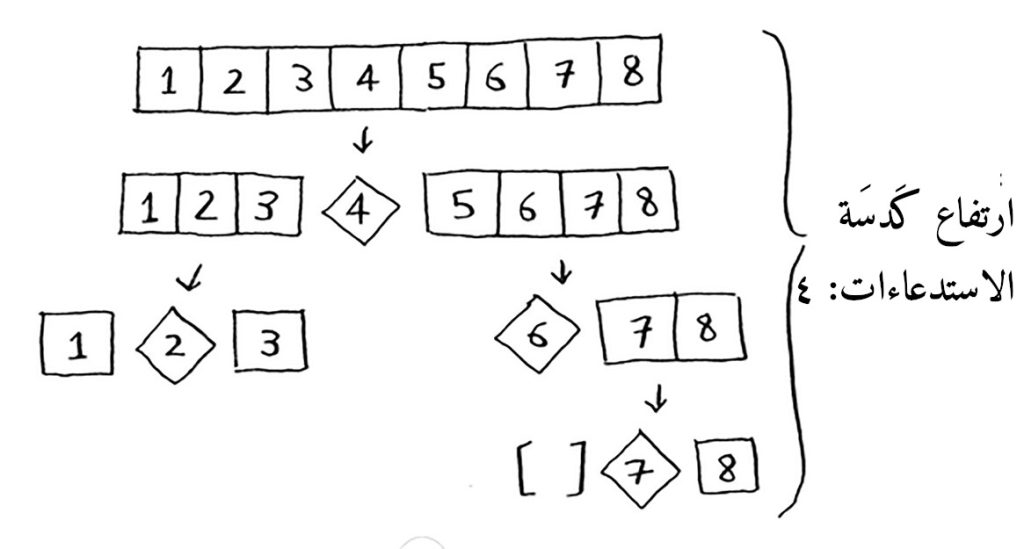
ارتفاعها منخفض، قصيرة جدا، لأنك تقسم الصفيفة من المنتصف كل مرة، وهذه هي الحالة الأحسن best case!

المثال الأول هو الحالة الأسوأ، لأن ارتفاع الكَدسَة فيه (س)O، أما المثال الثاني، الحالة الأحسن، فارتفاع الكَدسَة هو (لو س)O، لكن لِمَ؟

لنعد إلى المثال الأول، ونرى المستوى الأول في الكَدسَة. تختار العنصر الأول ليكون قيمة المُرتكَز وثم تقسم بقية العناصر إلى صفيفتين فرعيتين، وفي خِضمِّ ذا التقسيم في ذا المستوى من الكَدسَة، تتحقق من كل عناصر الصفيفة.

وهذا التحقق رمز O الكبير له هو (س)O.

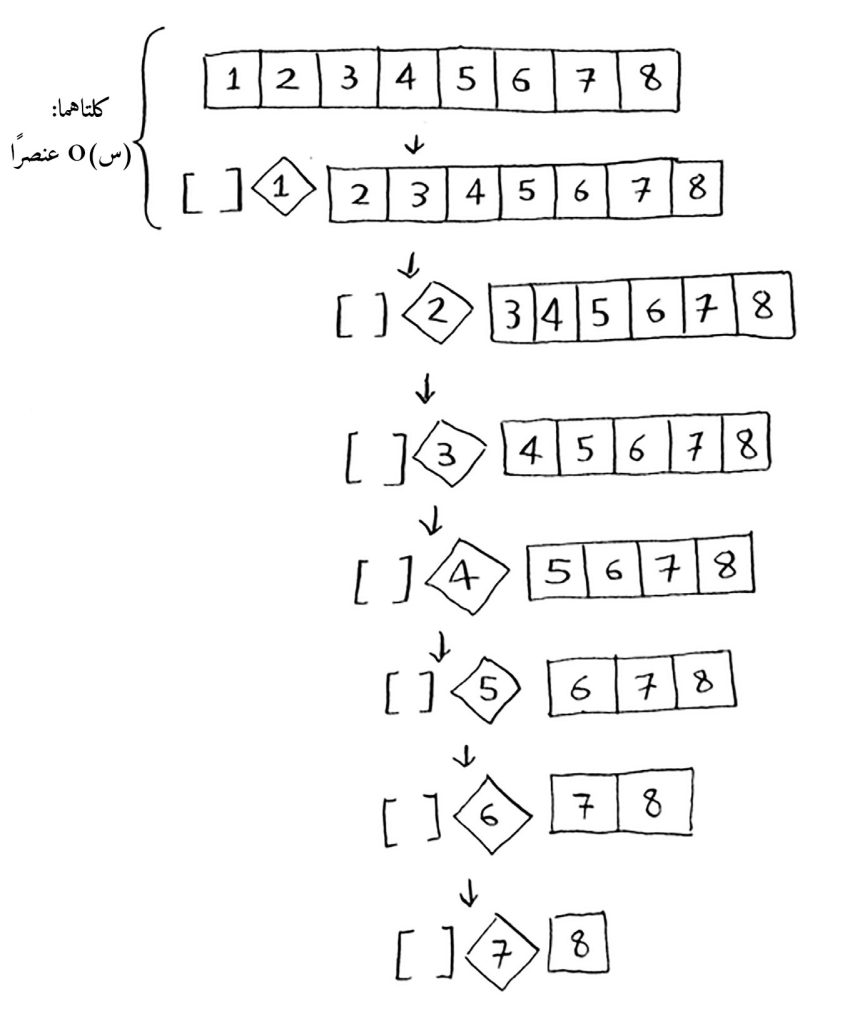
وحتى لو قسمت الصفيفة إلى جزئين من المنتصف وكانت قيمة المُرتكَز هي العنصر الأوسط في الصفيفة، فإن كل مستوى من الكَدسَة سيكون رمز O الكبير له هو (س)O.

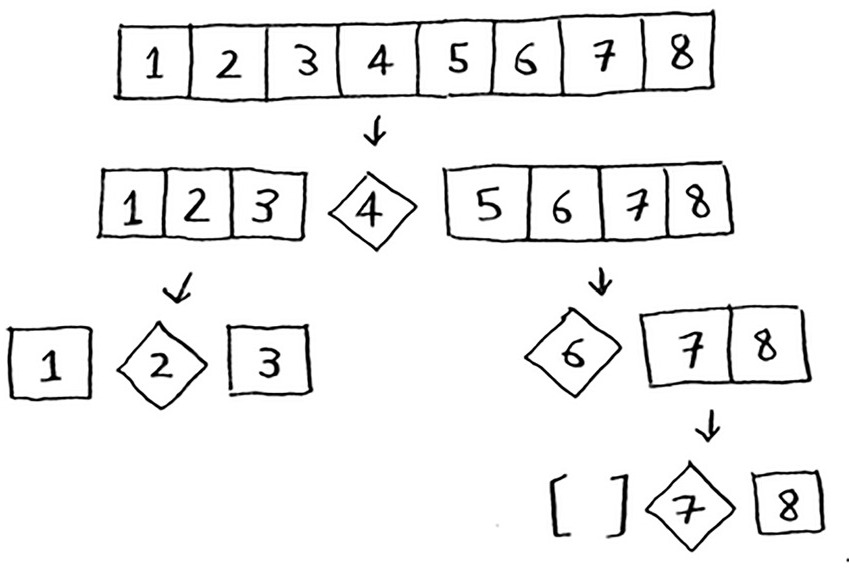
لذا فكل مستوى يستغرق (س)O للتحقق من كل عناصره:

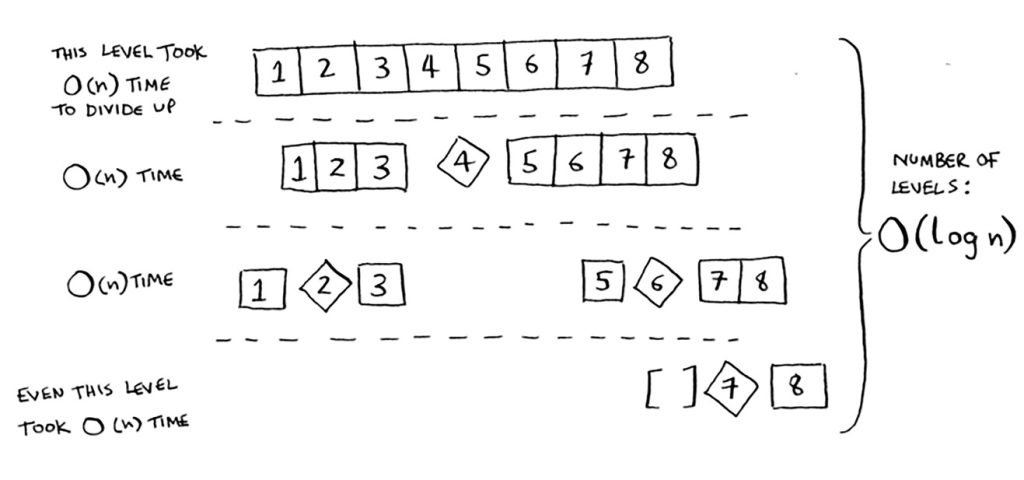
لكن لماذا عدد المستويات يساوي (لو س)O يا مبعسس! لم تخبرني!
سهل جدا، هذا شيء يتعلق بالرياضيات.
الصفيفة تساوي س، وفي كل مرة نقسم الصفيفة إلى جزئين، أي س قسمة ٢، وثم نكرر الخطوة من جديد، أي نعيد التقسيم س على ٢، وهكذا حتى نصل إلى جزء التوقف base case، أي أن النتيجة النهائية لهذا التقسيم تساوي ١.

انظر إلى الصورة:

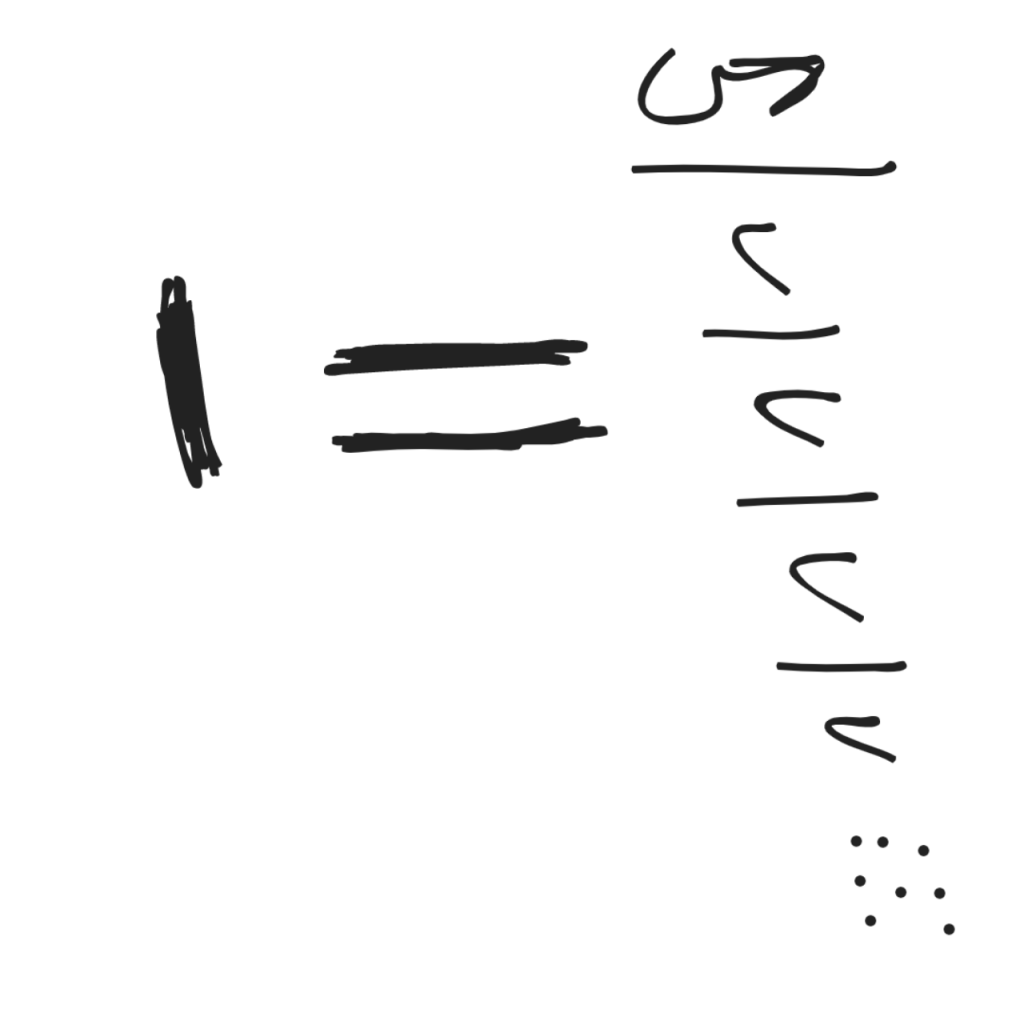
ولأن عدد المرات التي سنقسم فيها العدد س قد يكون أكثر من مائة مرة فإننا نقدر على اختصارها إلى هذه الصيغة: س قسمة ٢ أس ص تساوي ١:

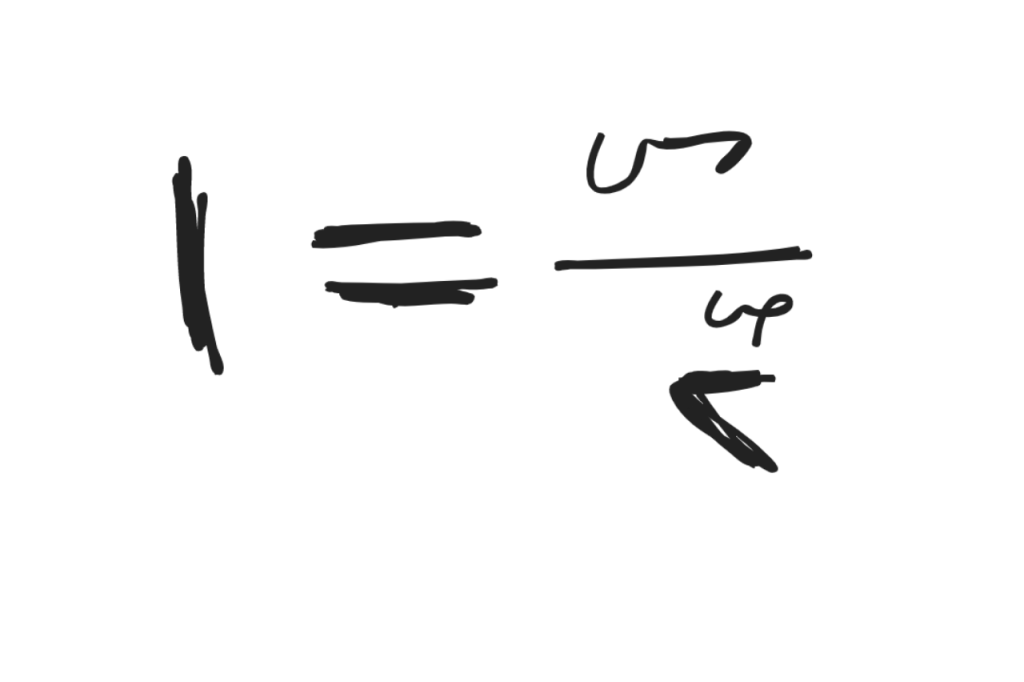
المتغير ص (صاد) هو عدد مرات القسمة التي سنقسم عليها العدد س على ٢. عين قيمة المتغير س برقم ١٦ واقسمه على الرقم ٢. كم مرة تحتاج فيها إلى قسمة العدد ١٦ على ٢ حتى تكون النتيجة هي الأحد ١؟
جرب على الورق، واحتفظ لهذه القيمة عندك.
الآن جرب هذه الصيغة المختصرة: س قسمة ٢ أس ص.

عين قيمة المتغير ص بالقيمة التي حصلت عليها، هل كانت النتيجة هي الأحد ١؟

لنتلاعب بهذه الصيغة، ففي الرياضيات فسحة لنا، حتى نصل إلى الصيغة المطلوبة وهي لو س.

لنضرب الوسطين في الطرفين، سنصل إلى هذه الصيغة:

 

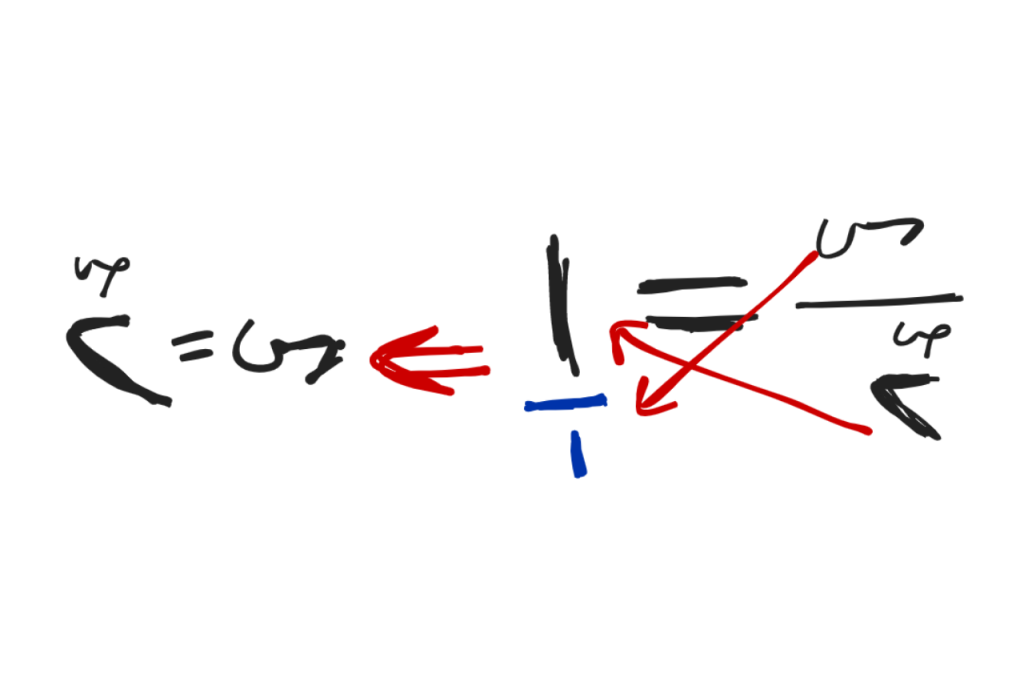
وهذه الصيغة لو راجعت درسنا الأول في شرح الكتاب، وفهمت الرياضيات فأنت تعلم بأنا نقدر على تحويلها إلى صيغة الأسيس (logarithm اللوغاريثم)، فما الأسيس إلا صورة مختلف للأس!
إذن ستكون الصيغة النهائية:

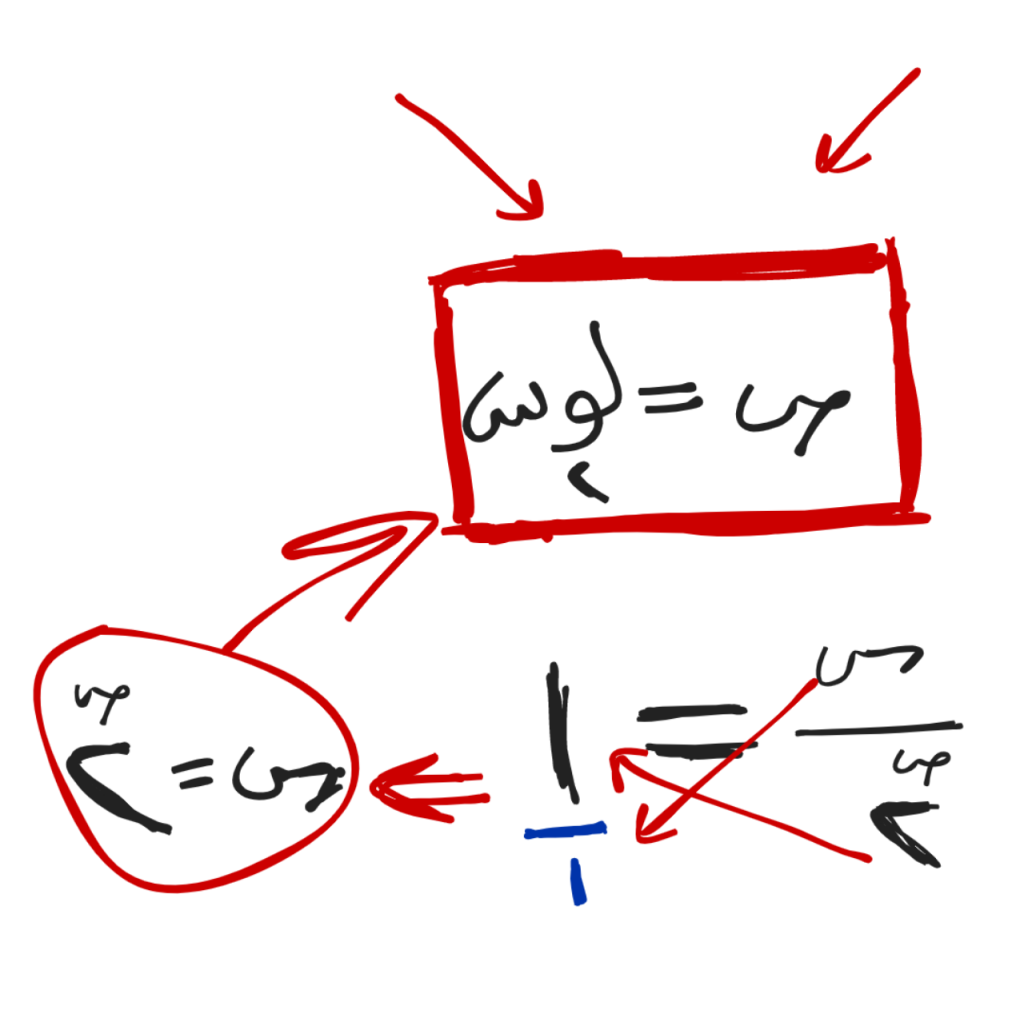
وكما قلت في المقال الأول إني سأستغني عن ذكر الأساس للأسيس الذي هو ٢، لأنه معلوم، لأنا نتعامل مع الحاسوب.

خلاصة الفقرة

في هذه الصورة:

عدد المستويات هو (لو س)O، تقنيا نقول: ارتفاع كَدسَة الاستدعاءات call stack هو (لو س)O. ورمز O الكبير في كل مستوى هو (س)O.

إذن:
(لو س)O × (س)O = (س لو س)O
وهذه هي الحالة الأحسن best case.

أما في الحالة الأسوأ: عدد المستويات (س)O، ورمز O الكبير في كل مستوى هو (س)O، إذن:
(س)O × (س)O = (س²)O

لكنك ستقول: ما مبعسس، هذه الخوارزمية مثل خوارزمية الفرز بالانتقاء في السرعة، فماذا أستفدت أنا بهذه الخوارزمية، تريد شرح مفهوم فَرِّق تَسُد لهذا أتيت بهذه الخوازرمية فحسب يا مخادع!

الأمر ليس كذلك البتة، هذه الخوازرمية من أسرع الخوارزميات، لأن الحالة الأحسن هي ذاتها الحالة المتوسطة average case للخوارزمية ما دمت:
١. تختار العنصر المتوسط في الصفيفة ليكون المُرتكَز،
٢. أو ما دمت تختار عنصرا عشوائيا ليكون قيمة المُرتكَز.

ففي المتوسط فإن الخوارزمية ستكون (س لو س)O ونادرا ما ستكون (س²)O، أي أنك نادرا ما ستواجه الحالة الأسوأ، نادرا جدا جدا!

اختيار المُرتكَز

كما سبق وقلنا، خوارزمية الفرز السريع فريدة لاعتماد سرعتها على اختيارك لقيمة المُرتكَز، فإن كان حَسَنًا ما اخترته كانت سريعة وإلا فالضِّد منه.

إذن كيف نختار قيمة المُرتكَز الفعالة؟
سبق وذكرت طريقتين في الأعلى، لكني سأعيد ذكرها:

١. نختار العنصر المتوسط في الصفيفة
٢. نختار عنصرا عشوائيا
٣. متوسط الثلاثة Median-of-Three: نختار القيمة المتوسطة بين ثلاثة عناصر هم: العنصر الأول في الصفيفة، والعنصر المتوسط، والعنصر الأخير.
٤. متوسط المتوسطات Median-of-Medians: نقسم اللائحة إلى مجموعات صغيرة، وثم نجد المتوسط لكل مجموعة، ثم نجد المتوسط لكافة المجموعات الصغيرة!

بخطوات واضحة:
أ. نقسم اللائحة إلى مجموعات صغيرة بقيمة ثابتة، مثلا لتكون خمسة عناصر أو تسعة مثلًا.
ب. نوجد الوسيط لكل مجموعة، والوسيط هاهنا، هو القيمة الوسطى عند ترتيب العناصر تصاعديا.
ج. نأخذ كافة المتوسطات في الخطوة ب، ونبحث عن متوسطها.

الخاتمة

ها قد وصلنا إلى نهاية مقالنا عن خورزمية الفرز السريع!

وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.

وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.

أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.