بسم الله الرحمن الرحيم
وردنا من متابع كريم قبل سويعات أن قد استشكل عليه الصف الدائري circular queue واستصعبه فلم يفهمه، وأنا مُفصِّلٌ له الأمر ومزيده بيانًا، فنحن في ركب مبعسس يمني يقف الركبُ جميعًا نصرةً لأخيهم، ونحن كما قال رسول الله صلى الله عليه وسلم: (مثل المؤمنين في توادهم وتراحمهم وتعاطفهم مثل الجسد إذا اشتكى منه عضو تداعى له سائر الجسد بالسهر والحمى).
المقال المذكور:
علة الصف العادي
اعلم أيها الكريم -أدام الله نعمته عليك- أن في الصف العاد علة اقتضت مجيء نوع جديد، هذه العلة إن برمجته بيدك تكشفت لك، وأنا كاشفها لك اليوم ثم مخبرك كيف عالجها أهل الصنعة بالصف الدائري.
قلنا الصف العادي بنية معطيات خطيَّة linear، ومعنى خطية (راجع الفصول الأولى) أن تكون على خط مجازًا، كالعِقد وانتظام الدرر في السلك (أي الخيط)، وليست المسبحة بغريبة عنك وأنت لا تقدر على انتزاع خرزة (حبة) من وسط المسبحة إلا وانتثرت خرزاتها وانقطع السلك الناظم لها، وبالمثل الصف Queue، فهو بمنزلة السلك للخرزات، والعناصر في الصف هي الخرزات في السلك.
وبرمجته إن شاء الله سهل، إذ سنمثل السلك بالصفيفة array والخرزات بالعناصر Items، وننظم الخرزات في السلك، ولاحظ كيف يبرمج المبرمج، إذ ينتزع المعاني من واقعه بتفاصيلها الدقيقة ثم يقذف بها في برنامج بديع السبك.
عندنا سلك يتسع لست خرزات، وبلغة أهل البرمجة عندنا صفيفة تتسع لستة عناصر:
(_, _, _, _ ,_ , _)هذه الصفيفة فارغة والشرطات السفلية لأخبرك بأن كل خانة فارغة.
السؤال الآن، كيف ستعرف أين بداية الصفيفة وأين نهايتها؟ أين الرأس من الذيل؟ بل أين بداية السلك من نهايته؟
فالسلك له بداية تدخل منها الخرزات ثم نهاية تخرج منها الخرزات. أنت بعقلك تعرف أين بدايته من نهايته، وتعرف أي خرزة ستخرج أولًا وتعرف أي خرزة كانت الأخيرة في السلك قبل عقد طرفيه حتى يصير السلك عِقدًا تتحلى به المرأة العاطِل (العاطِل من النساء التي ليس في عُنُقها حَليٌ)، لكن في البرمجة برنامجك لا يعقل شيئًا إلا ما أمرته، وعليك أن تُفصِّل فتذكر كل تفصيل، ومن هنا أتيتَ فلم تفهم.
إذن لا بد من إنشاء مُتغيرين، الأول يدلنا على بداية السلك وسنسميه front (ومعناه المقدمة)، والآخر يدلنا على نهايته وسنسميه rear (المؤخرة)، لأننا إذا أردنا الإضافة سنذهب ونرى أين نهايته؟ ونضيف العنصر (والتي مثلناها بالخرزة) إلى هذه النهاية، وإذا أردنا الحذف سنذهب ونرى أين بدايته؟ ونحذف العنصر من بدايته، اتباعًا لمنهج (أول وارد هو أول صادر)، فأول من يأتي هو أول من يُخدم ثم يمضي في سبيله (نقول في العامية: الأول فالأول).
هذان المتغيران تتحدث قيمتهما عند كل إضافة أو حذف، وهذا منطقي، فإن لم تحدث قيمتهما في كل مرة فإنه سيدلنا على مكان قديم، وهذا لا يصح البتة. افهم هذه الجزئية من برمجته فإنها ستعرفك بالعلة، تابع القراءة…
إذا كانت الصفيفة فارغة فبأي قيمة نهيِّئ المتغيرين؟ أي شيء سيحويا في داخلهما والصفيفة فارغة؟
سنهيِّئ المتغيرين بقيمة سالب واحد -١، ومعناه أول عنصر في الصفيفة، وقد درست ذلك في بايثون:
[_, _, _, _ ,_ , _]
front = -1, rear = -1سنضيف رقمًا إلى الصفيفة وننظر كيف ستتغير قيمة المتغيرين: المقدمة front والؤخرة rear:
[10, _, _, _, _, _]
front = 0, rear = 0لِمَ الصفر؟
لأنك تعلم أن العد يبدأ من الرقم صِفر في لغات البرمجة، فالمتغير الأول قيمته الصِفر لأنه أول عنصر في الصفيفة، والمتغير الآخر قيمته الصِفر أيضًا لأنه آخر عنصر في الصفيفة، فذاك الرقم هو أول خرزة في السلك وآخر خرزة في الوقت نقسه. اعذرني عن التفصيل الممل لكن لا بد منه لتفهم الأمر.
سنضيف العدد الثاني الآن وننظر في قيمة المتغيرين:
[10, 20, _, _, _, _]
front = 0, rear = 1قيمة المتغير الأول، وهو المقدمة front، لم يتغير، بل الذي تغير كان المتغير الثاني، متغير المؤخرة rear، وهذا منطقي لأن متغير المقدمة يشير دومًا إلى العنصر الذي أُدخِل أول مرة، فهو لا يتغير في الإضافة، إنما الذي يتغير هو المتغير الثاني حتى يدلنا على مؤخرة الصف، أي آخر عنصر في الصف، وهو في مثالنا هذا قيمته الواحد الصحيح، والذي يدل على العنصر الثاني في الصفيفة.
سنضيف عنصرًا ثالثًا:
[10, 20, 30, _, _, _]
front = 0, rear = 2كما ترى أمامك تغير المتغير الثاني وهو المؤخرة rear إلى القيمة ٢، والذي يدل على العنصر الثالث في الصفيفة، ففي كل إضافة يتغير متغير المؤخرة فقط حتى يدل على آخر عنصر أضيف إلى الصف.
رأينا الإضافة والآن الإزالة، سنزيل العنصر الأول من الصفيفة ثم ننظر في قيمة متغير المقدمة:
[_, 20, 30, _, _, _]
front = 1, rear = 2أزلنا أول عنصر في الصفيفة وصارت أول خانة فارغة من العناصر، وتغيرت قيمة متغير المقدمة front إلى الواحد الصحيح الذي يدل على ثاني عنصر في الصفيفة وهو ٢٠.
اقرأ بتمعنٍ هنا حتى تبصر العلة بعينك، انظر كيف أن أول خانة صارت فارغة، وإن أزلنا عنصرًا آخر ستبقى خانته فارغة:
[_, _, 30, _, _, _]
front = 2, rear = 2أول خانة فارغة وثاني خانة فارغة، وقيمة متغير المقدمة front تغير إلى الرقم ٢ الذي يدل على العنصر الثالث في الصفيفة وهو ٣٠. وإذا أضفت عنصرًا فلن يُضاف في أول خانة فارغة، بل سينظر في قيمة متغير المؤخرة rear وثم يضيف العنصر بعد، وسيكون هكذا:
[_, _, 30, 40, _, _]
front = 2, rear = 3هل رأيت الخانات الفارغة؟ تبقى فارغة!
يتقدم متغير المقدمة دومًا للأمام أما متغير المؤخرة فلا يعود للخلف إلى الخانات الفارغة، مصيبة!
إذا امتلأ الصف ووصل متغير المؤخرة إلى منتهاه فلن يعود إلى البداية وفيها خانات فارغة، بل سيصيح: امتلأ الصف! امتلأ الصف!
وهذه العلة، فهو يسيء استعمال الذاكرة ويترك خانات فارغة بلا استعمال ولا يستعملها، فهو ليس كما ظننتَه أنت أنه في كل إزالة تتقدم المتغيرات إلى الخانة الفارغة كما في الواقع يتقدم الرجل بعد الرجل، لا، الحواسيب غبية وعليك تعليمها كل شيء!
بعد هذا التفصيل الممل استوعبتَ لا ريب، وأعلم أنك ستسأل الآن: ما علاج هذه العلة؟
علاج هذه العلة كان بمجيء نوع أحدث من الصف يعالج العلة في أخيه الأول، وقد كان هذا النوع هو الصف الدائري!
الصف الدائري
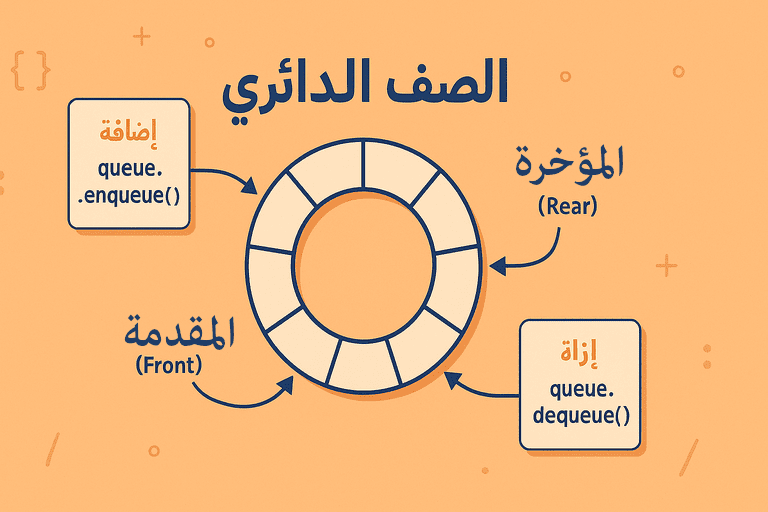
قد قلت في المقال الأول في تعريفه: آخر عنصر في هذا الصف يشير إلى أول عنصر، فيتكون رابط يربط بين أوله وآخره كأنه حلقة.
لماذا يشير أول عنصر إلى البداية عند أول عنصر؟ وكيف سيُربَط بين آخره وأوله؟
علاج العلة في الصف العادي كان أن يدوره جاعلينه دائرة، آخر يتصل بأوله، وهكذا عالجوا تلك العلة، فمتغير المؤخرة لن يقف في النهاية دون استعمال الخانات الفارغة في أول الصف، بل سيصل إلى النهاية في يلتف عائدًا إلى البداية، هذا جواب السؤال الأول.
أما السؤال الثاني: كيف ربطوا بين آخره وأوله: كان بباقي القسمة في الرياضيات!
لا تخف، الأمر سهل بلا تعقيد رياضي، عندك عشرة أولاد وألف ريال، كيف ستقسم الألف عليهم؟
ستعطي كل صبي مئة ريال. وإذا كان عندك ثلاثة أولاد ومعك ألف ريال وقلت لك قسمها عليهم؟
ستعطي كل واحد ثلاثمئة ريال وتبقى معك مئة ريال، إذن فباقي القسمة مئة ريال.
سهل والله! واصل القراءة…
الصف السابق كان يتسع لست خانات، والعد في لغات البرمجة يبدأ من الصفر، إذن سيصل متغير المؤخرة rear إلى آخره إذا وصل إلى الرقم ٥، احسبهم:
0 -> 1 -> 2 -> 3 -> 4 -> 5كل مرة نضيف فيها عنصرًا سنطبق فيها المعادلة السهلة الآتية:
rear = (rear + 1) % size_of_queueمتغير المؤخرة rear معروف، متغير فيه دليل index آخر عنصر (الدليل ترجمة index)، سنأخذ هذا المتغير ونضيف عليه واحدًا ثم نأخذ الناتج ونوجد باقي قسمته على حجم الصف size_of_queue.
سنطبق المعادلة على الصف السابق الذي يتسع لست خانات (حجم الصف = ٦)، وسنقول إنه قد امتلأ، ثم ننظر هل المعادلة ستربط آخر عنصر بأول عنصر أم لا!
قيمة متغير المؤخرة = ٥ (امتلأ الصف)
قيمة متغير حجم الصف = ٦
طبق المعادلة وسترى الناتج كان الصفر، أي أول عنصر في الصفيفة!
rear = (rear + 1) % 6 → (5 + 1) % 6 = 0ستة قسمة ستة لن يبقى أي شيء، صِفر!
يشبه الساعة على الجدار أو في هاتفك، كلما وصلت إلى الساعة ١٢ تنقلب إلى الساعة ١، وهذا بنفس المعادلة:
(12 + 1) % 12 = 1لأن باقي قسمة ١٣ على ١٢ يساوي ١ (اثنا عشر طفلًا وعندك اثنتا عشرة تفاحة قسمتهن عليهم، سيتبقى عندك تفاحة واحدة).
سمها معادلة سحرية إن شئت، لا بد من رياضيات أن أردت تصبح من أهل القوم، ففي الأشياء المتقدمة لا بد من رياضيات!
الواجب
واجب اليوم أن تبرمج الصف الدائري بنفسك! سهل والله، إضافة صغيرة عن صف الأمس، نضيف إليها المعادلة التي تعلمناها اليوم لجعله دائريًا.
لا تنظر لهذا الحل إلا بعد المحاولة بنفسك ثم مقارنة حلك بهذا الحل وانظر ما زدتُ -أنا- عليه، وادرسه فأنت إن شاء منتفعٌ به.
class CircularQueue:
def __init__(self, size):
self.size = size
self.queue = [None] * size # initialize the queue with None
self.front = -1
self.rear = -1
def is_full(self):
# Queue is full if next position of rear is front
return (self.rear + 1) % self.size == self.front
def is_empty(self):
# Queue is empty if front is -1
return self.front == -1
def enqueue(self, value):
if self.is_full():
print("Queue is full! Cannot enqueue.")
return
# First insertion
if self.is_empty():
self.front = 0
# Move rear forward circularly
self.rear = (self.rear + 1) % self.size
self.queue[self.rear] = value
print(f"Enqueued: {value}")
def dequeue(self):
if self.is_empty():
print("Queue is empty! Cannot dequeue.")
return None
value = self.queue[self.front]
self.queue[self.front] = None # Optional: clear slot
# If queue becomes empty after this dequeue
if self.front == self.rear:
self.front = -1
self.rear = -1
else:
# Move front forward circularly
self.front = (self.front + 1) % self.size
print(f"Dequeued: {value}")
return value
def display(self):
if self.is_empty():
print("Queue is empty.")
return
print("Queue contents:")
i = self.front
while True:
print(self.queue[i], end=" ")
if i == self.rear:
break
i = (i + 1) % self.size
print()
الخاتمة
ها قد وصلنا إلى نهاية المقال، وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في الشرح.
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.