بسم الله الرحمن الرحيم
هذا الدرس الثالث من تلخيص كتاب الساحر، الذي قد بدأناه وهذه مقدمته:
الدرس السابق:
عرفنا فيما مضى التجميعة combination واليوم نغور إلى كُنْهِها ونرى سبر أغوارها، كيف تُعالج وتُنَفَّذ. الأمر سهل يسير، فالتجميعة تمر بخطوتين لا غير!
لما يرى المفسِّر تعبيرًا أو تجميعة من التعابير فإن يتبع هاتين الخطوتين، وهي قاعدة تنفيذ التعبيرات:
١. نفذ التعابير الفرعية للتجميعة أولًا، أي ننفذ كل معمول operand،
٢. ثم طبق العامل operator على نتيجة العمل في الخطوة الأولى.
سهل؟ نضرب مثالًا؟
سنسير على مهلٍ وأناة، حتى نفهم كيف يعمل المفسر interpreter لما نكتب تعبيرًا، وثمرة ذلك = فهم مكين لأسلوب البرمجة الوظيفي/إجرائي.
لما نكتب تعبيرًا فإن المفسر interpreter يطبق وظيفة procedure على التعبير المدخل (القاعدة المذكورة المكونة من خطوتين)، وهذه الوظيفة هي ما تقدم ذكره (الخطوة الأولى والثانية، القاعدة).
تعبير بسيط
سنطبق الخطوتين على التعبير الآتي:
(+ 2 3)الخطوة الأولى (نفذ التعابير الفرعية للتجميعة أولًا، أي ننفذ كل معمول operand)، والتعابير الفرعية هاهنا هي الرقم ٢ والرقم ٣، فالعامل + يتعدى إلى معمولين.
وكما عرفنا في التلخيص الثاني، فإن الرقم ٢ تعبير يفهمه المفسر، فهو تعبير يمثل عددًا، لذا فالخطوة الأولى سترجع نفس القيمة، وتنتهي هنا.
تنفيذ الرقم ٢ ← يرجع الرقم نفسه
تنفيذ الرقم ٣ ← يرجع الرقم نفسه
ناتجها إرجاع الرقمين كما هما.
الخطوة الثانية (ثم طبق العامل operator على نتيجة العمل في الخطوة الأولى)، العامل معنا هو الجمع +، وسنطبقه على معمولين، الرقم ٢ والرقم ٣، سنجمعها، وناتج هذه الخطوة الرقم ٥.
طبق معامل الجمع + على المعمولين (٢ + ٣) ← ٥، انتهى.
تعبير مركب (تركيبة)
نرتقي بالصعوبة قليلًا ونطبق الخطوتين على تعبير مركب، وقبل الشروع أجبني: أتحسب الخطوتين كافيتين أم أننا سنبتدع خطوة ثالثة ورابعة كلما زاد التعبير تعقيدًا؟
لا تخبرني بالجواب، سنطبق ونتحقق 🙂
التعبير المركب الآتي:
(* (+ 6 7) 4)سنطبق الخطوة الأولى القائلة: (نفذ التعابير الفرعية للتجميعة أولًا، أي ننفذ كل معمول operand)، والتعبير المركب الآنف ذكره، يتكون من تعبيرين هما: (7 6 +)، و4.
وأول تعبير هو القوس الذي فيه الجمع:
(+ 6 7)هذه المرة لم تكن التعابير سهلة مثل التعبير الذي يمثل عددًا فنرجع نفس العدد، لا، هذا القواس ومحتواه يريد إلى تنفيذ أيضًا، فهو تعبير يحوي في داخله تعابير فرعية (الرقم ٦ والرقم ٧)، فما الحل؟
أتحسبني سأبتدع خطوة ثالثة لأحل المسألة؟
لا يا صاحبي، سأستدعي الخطوتين مرة ثانية، وستبدأ من الخطوة التي تقول: (نفذ التعابير الفرعية للتجميعة أولًا، أي ننفذ كل معمول operand)، وسأطبقها على التعبير الفرعي (7 6 +).
هذه الخطوة ستأخذ المعمولين ٦ و٧، وترجعمها. ثم سأطبق العامل + عليهما، ونتيجته ١٣.
ثم سنعود إلى التركيبة التي كانت:
(* (+ 6 7) 4)ونستبدل القوس (7 6 +) بالناتج ١٣، بعد تطبيق الخطوتين عليه، وسيصبح:
(* 13 4)والآن سنطبق الخطوتين مرة ثانية، وسيكون الناتج ١٧.
لا تبتئس إن تُهتَ وما فهمت، سنسهل الأمر ونشجر المقال الآتي، تمثيل شجري (ابحث عن tree accumulation):
(+ 2 (* 3 4))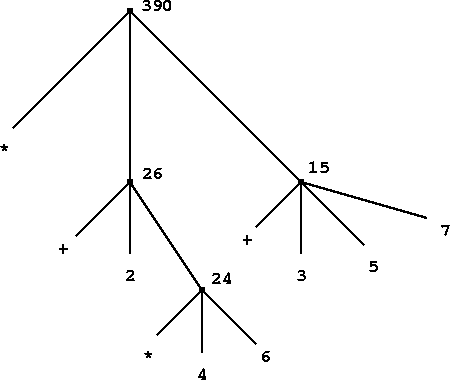
وتمثيله شجريًا:
+
/ \
2 *
/ \
3 4
الشجرة تنقسم إلى ثلاثة أقسام:
الجذر root: وجذر الشجرة المعامل +
الفروع: قد تكون ذات فرع واحد أو أكثر، وكله بحسب المعمولات الموضوعة، وشجرتنا التي فوق ذات فرعين، لأنها ذات معمولين فقط. وقد تكون هذه الفروع تحوي فروعًا أخرى وهكذا…
الغصون: والغصن ما يتدلى من الفرع وينتهي.
لنحل المثال!
سنبدأ من الجذر، والذي هو المعامل +، ومنه سننزل إلى الفروع، فرعًا فرعًا، نطبق في كل مرة الخطوتين.
سننزل من الجذر إلى الفرع الذي هو الرقم ٢، ونطبق الخطوة الأولى، والناتج سيكون الرقم نفسه. هل يحوي هذا الفرع على فروع أو أغصان؟
لا، إذن نتوقف هنا، ونتجه إلى الفرع الذي يليه.
الفرع الذي يليه يحوي غصنًا، وهو:
*
/ \
3 4
وبما أنه يحوي غصنًا، فإننا سنصيره شُجيرة لوحده، وجذر هذه الشجيرة المعامل *، وفروعها الرقم ٣ والرقم ٤.
وهنا نحتاج إلى استدعاء الخطوة الأولى، التي ستنفذ التعابير الفرعية (الرقم ٣ والرقم ٤)، وسترجعهما كما هما لما تفرغ من تنفيذهما، ثم بعدها نستدعي الخطوة الثانية التي تطبق المعامل وهو معامل الضرب على هذه التعابير الفرعية:
٣ ضرب ٤ = ١٢
النتيجة النهائية ١٢، لا تنس أنا في الغصن الذي صيرناه شُجيرة، وهذه نتيجته.
الآن سنعود إلى الشجرة الأصلية ونستبدل ذاك كله بالعدد ١٢:
(+ 2 12)تلخيصات
لاحظت أننا عند تطبيق الخطوة الأولى فنحن نفكك التركيبة ونعود بها إلى المكونات الأساسية، مثل الأرقام والوظائف الأساسية وأسماء المتغيرات. تلخيصات
نستلخص مما تقدم أن:
أ. قيمة الأعداد ترجع كما هي.
ب. قيمة الوظائف الأساسية (جمع وطرح إلخ…) ليست إلا سلسلة تعلميات للآلة.
جـ. قيمة المتغير هي ما يحويه، لأن المتغير ليس إلا علبة، والقيمة داخله.
أنواع على رأسها ريشة
بعض الأنواع في لغة Lisp لا تخضع للقاعدة المذكورة في البداية، بل لها قاعدة خاصة بها، وكأن على رأسها ريشة، أميرة تتميز عن غيرها، واسمها أنواع خاصة special forms.
أول نوع من الأنواع الخاصة تعليمة التعريف define: إذ لا تخضع للقاعدة، فإنها تربط اسم المتغير بقيمة، فالمتغير ذاك هو نفسه القيمة المسندة إليه، لكن الاسم يسهل لنا نحن البشر البرنامج (تعليمة التعريف ليس تجميعة combination).
وذكر في المحاضرة الثانية نوعين آخرين: العبارات الشرطية وشيء اسمه Lambda، نسميها في البرمجة الوظيفة المجهولة. وليس هذا مقام شرح النوعين، أرجأت شرحمها إلى مكان آخر.
وقبل الختام: هل اندهشت أن المفسر interpreter لا يتبع سوى قاعدة سهلة؟
لا شك أنك حسبت العملية التي يؤديها المفسر عملية معقدة، لكن تبين لك الآن سهولتها، فنفس الخطوات تتكرر.
نستلخص مما تقدم مبدأ هام كل الأهمية، ألا وهو العَودية (بفتح العين، من العودة والتكرار)، والعَودية recursion: استدعاء الوظيفة لنفسها. كما فعلنا آنفًا واستدعينا نفس الخطوات، والوظيفة قد تستدعي نفسها مرات ومرات. وهذا المبدأ على سهولة فهمه عند كثير من الناس = سهل مُمْتَنِع، يفهمونه ويعجزون عن استعماله.
سر خطير: باستعمال هذه المبدأ سنبني حلقة التكرار بأيدينا.
ووجب الذكر أن العَودية تُذكر مقترنة مع مبدأ آخر اسمه (فَرِّق تَسُد Divide and Conquer) حتى يَسْهُل فهمها، وقد سبق لي شرحهما في الموقع:
سنتعرض للعَودية في الباب الأول كثيرًا، فإن لم تفهمها فلا تبتئس، نحرق الكتاب ولا نراك بائسًا. 🙂
الخاتمة
وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق!
وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.
أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.