بسم الله الرحمن الرحيم

انتهينا من الفصل الأول، فصل (لبنات لغة البرمجة)، ولله الحمد، فإن نسيته راجعه، فهو الأساس الذي نبني عليه، واليوم الفصل الثاني، فصل (الوظائف والعمليات الخارجة منها).

كما قرأت، أساس نبني عليه، ليس بكافٍ البتة لنقول إنَّا نعرف البرمجة. شبه الكاتب من درس الفصل الأول بمن يعرف قواعد الشطرنج فقط، كيف يحرك القطع، لكنه يجهل الافتتاحيات والنهايات، أولم تكُ تدري أن لاعبي الشطرنج يفتتحون اللعبة بافتتاحات معروفة مشهورة؟

مثلا الافتتاح الإسباني والافتتاح الإيطالي والدفاع الفرنسي والروسي، ودفاع الملك الهندي، وقد ترى تفريعات لما سبق، ثم ينتقلون من الافتتاح إلى وسط الدور فالنهايات.

وبالمثل، فالمبرمج المبتدي يعرف نحو اللغة Syntax، كلاعب الشطرنج المبتدي الذي يعرف كيف يحرك القطع، لكنه لا يعرف النهج الذي يجب اتباعه عند حله لمشكلة. وقلت لك (النهج)، لأن النهج المتبع عند حل مشكلة يختلف وله بليغ تأثير. 

النهج المتبع ليس إلا نمطًا قد تكرر واستعمله أهل هذا الفن وتعارفوا عليه. أول أغراض هذا الفصل أن نتعرف على بعض هذه الأنماط patterns. عند تنفيذك لوظيفة فإن العملية التي ستصدرها هذه الوظيفة قد يكون نهجًا/نمطًا معروفًا، ولعل أهل هذا الفن عندهم نهج آخر أحسن من الأول.

أما الغرض الثاني أن نكون على أتم الإدراك بالأثر المترتب عند تنفيذ وظيفة، أي عواقب الأمور ومآلها، وبلغة السحرة: أن ندرك عواقب استحضار هؤلاء المردة. غير كافٍ أن تعمل الوظيفة فحسب، بل عليها أن تبلي بلاءً حسنًا في برنامج أو نظام كبير دون تعطيل لغيرها عن عملها. وهذا لا محالة يستلزم أن تفهم كيف ستعمل وظيفتك وأي سلوك ستسلكه، فتنبَّه!

قال ابن الجوزي رحمه الله في كتابه (صيد الخاطر):

 

«من عاين بعين بصيرته تناهي الأمور في بداياتها نال خيرها ونجا من شرها، ومن لم ير العواقب غلب عليه الحس، فعاد عليه بالأسلم ما طلب منه السلامة، وبالنصب ما رجا منه الراحة».

وقال ابن الجوزي رحمه الله:

 

راقب العواقب تسلم، ولا تمل مع هوى الحس فتندم.

أول نمط، وسأسميه نهجًا، هي العَودية (بفتح العين)، والثاني التكرار.

 العَودية

تعرضنا لمفهوم العَودية فيما مضى، وأنها: استدعاء الوظيفة لنفسها. أما اليوم سنرى مثالا ونتحدث في العَودية، ونناقش أمرًا آخر اسمه التكرار iteration.

أول مثال: العاملي factorial.

عاملي العدد ٤ هو ضرب كل الأعداد الموجبة الأصغر من ٤، ما عدا الصِفر. ويُمثَّل بوضع علامة تعجب قبل العدد.

س! = س × (س – ١) × (س – ٢) × … × ١

مثلا عاملي العدد ٤: 

س = ٤

4! = 4 × (4-1) × (4-2) × (4-3)

==> 4! = 4 × 3 × 2 × 1

==> 4! = 24 

إذن عاملي العدد ٤ يساوي ٢٤. كيف نثمله باستعمال العَودية؟

سنقول:

س! = س × (س-١)!

لاحظ، سترى أننا وضعنا علامة تعجب بعد القوس، كأننا نقول: لكي نحسب س! علينا أولًا حساب (س-١)!، ثم نضرب الناتج في س. 

لو كان نريد عاملي العدد ٤ باستعمال القاعدة الآنف ذكرها:

4! = 4 × (4-1)!

لدينا العاملي الأول ٤!، ثم العاملي الثاني (٤-١)!، فلا بد من تنفيذ العاملي الثاني الذي ظهر، لذا نستكمل سير العملية:

==> 4! = 4 × 3!

==> 4! = 4 × (3! = 3 × (3-1)!)

==> 4! = 4 × (3! = 3 × 2!)

==> 4! = 4 × (3! = 3 × (2! = 2 × (2-1)!))

==> 4! = 4 × (3! = 3 × (2! = 2 × 1!))

وصلنا إلى عاملي الواحد، وهنا نقف، لأن الصفر أصغر من الواحد، وما تحت الصفر عدد سالب، وهذا يخالف قاعدة العاملي لو واصلنا إلى السالب، لكن نقف هنا. شرط التوقف الذي يوقف الوظيفة اسمه base case، نترجمه إلى شرط التوقف.  🙂

هيا نستكمل سير العملية:

==> 4! = 4 × (3! = 3 × (2! = 2 × 1))

==> 4! = 4 × (3! = 3 × (2! = 2))

==> 4! = 4 × (3! = 3 × 2)

==> 4! = 4 × (3! = 6)

==> 4! = 4 × 6

==> 4! = 24

سرتُ بالتفصيل لتفهم، وكله إلى الآن حبر على الورق، فهيا نمثله باستعمال ما تعلمنا في الفصل الأول من الباب الأول. سنكتب وظيفة لتحسب لنا العاملي، وهذه الوظيفة تستقبل عددًا، وترجع لنا عاملي العدد. هنا الرماز:

(define (factorial number)
  (if (= number 1)
      1
      (* number (factorial (- number 1)))))

تخبرنا الوظيفة عن أمرين:

أ. شرط التوقف base case: هو أن يكون المدخل يساوي الواحد (1! = 1، أي عاملي الواحد هو الواحد، قف هنا).

ب. شرط العَودة recursion case: أن لا يساوي المدخل الواحد، وفي هذه الحالة تستدعي الوظيفة نفسها لكنها تنقص من المدخل س رقمًا واحدًا.

(factorial (- number 1))

وما سبق يجب أن تحويهما الوظيفة العَودية، لأنها بلا الشرط الأول، شرط التوقف فستعمل بلا توقف، أما لو عملت بلا الشرط الثاني فإنها ستتوقف لا محالة، كيف تستدعي نفسها؟

لا تنسهما!

سنشغل الوظيفة الآن ونمرر لها ٦. 

 بتطبيق وحدة التعويض substitute model سيتضح الأمر وتفهم:

(factorial 6)
  (* 6 (factorial 5))
  (* 6 (* 5 (factorial 4)))
  (* 6 (* 5 (* 4 (factorial 3))))
  (* 6 (* 5 (* 4 (* 3 (factorial 2)))))
  (* 6 (* 5 (* 4 (* 3 (* 2 (factorial 1)))))))
  (* 6 (* 5 (* 4 (* 3 (* 2 1)))))
  (* 6 (* 5 (* 4 (* 3 2))))
  (* 6 (* 5 (* 4 6)))
  (* 6 (* 5 24))
  (* 6 120)
  720

 استدعاء الوظيفة مع المدخل ٦ ←← يستدعي الوظيفة نفسها مع المدخل ٥، وهكذا…

هذا النمط يتكرر ويتكرر حتى تصل الوظيفة إلى شرط التوقف وهو أن يكون المدخل يساوي الواحد، واسمه عَودية خطية liner recursion. استدعاءات متداخلة، كل استدعاء يُوضع على أخيه، تكديس، ولما تنتهي كل الاستدعاءات = تُضرب نتيجة آخر استدعاء بما يسبقه وهكذا… حتى تُطبع النتيجة.

التكرار iteration 

سنطبق العاملي باستعمال نهج مختلف (نمط)، اسمه التكرار، وسنصل إلى نفس النتيجة باستعماله.

هذه المرة لن ننتظر الوظيفة حتى تصل إلى شرط التوقف لتبدأ ضرب الأعداد، لا، بل سنضرب كل عدد قبل الانتقال إلى الخطوة التالية.

مثلًا عاملي العدد س، وليَكُن ٤:

ضرب العدد ٤ بالرقم ١، ثم ضرب الناتج بالرقم ٢، ثم ضرب الناتج بالرقم ٣، وتتوقف عن الضرب لما تصل إلى س، وهو في حالتنا ٤، لهذا توقفنا.

كيف سنمثل الأمر برمجيًا؟ تفكر قبل المواصلة

ضربنا العدد المدخل في رقم (المدخل: ٤، وضربناه في ١ إلى ٣)، ثم ضربنا حاصل الضرب للخطوة السابقة في رقم آخر وهكذا..

أي: نضرب في كل مرة حاصل ضرب المدخل في رقم جديد، ضربنا المدخل ٤ في ١، حاصل ضربهما ٤، ثم ضربنا حاصل الضرب في ٢، وحاصل ضربهما ٨. وأظنك لاحظت أننا نخزن حاصل الضرب، ثم نضربه في الرقم الجديد، وهذا أول متغير وهو المتغير الذي يخزن لنا حاصل الضرب في كل مرة، ونسميه product.

ركز، قلنا نضرب حاصل الضرب في (رقم جديد)، فمن أين يأتي ذا الرقم وأين يُخزَّن؟

سننشئ نحن متغيرًا، نسميه العدَّاد counter، سيُهيَّأ بالقيمة ١، وفي كل مرة تتغير قيمته بمعدل رقم كل مرة. يبدأ بالقيمة ١، وفي الخطوة الثانية تكون قيمته ٢، وهكذا. هذا رمازها:

(define (factorial-iter number)
  (define (iter counter product)
    (if (> counter number)
        product
        (iter (+ counter 1) (* counter product))))
  (iter 1 1))

 

ألخِّص لك ما ستؤديه الوظيفة:

١) تستقبل عددًا، ٢) وتنشئ متغيرين،

المتغير الأول (حاصل الضرب) وقيمته: ضرب العداد في حاصل الضرب نفسه!

والمتغير الثاني (العدَّاد)، وقيمته: العداد زائدًا الواحد،

 ٣) وثم ستبدأ السير في حلقة من التكرار، وأمامك شرط التوقف وشرط العَودية، أتركهما لك.

سننفذ الوظيفة وسنرى سير عملها، فلاحظ الفرق بين هذا النهج والنهج السابق، هذا النهج هكذا:

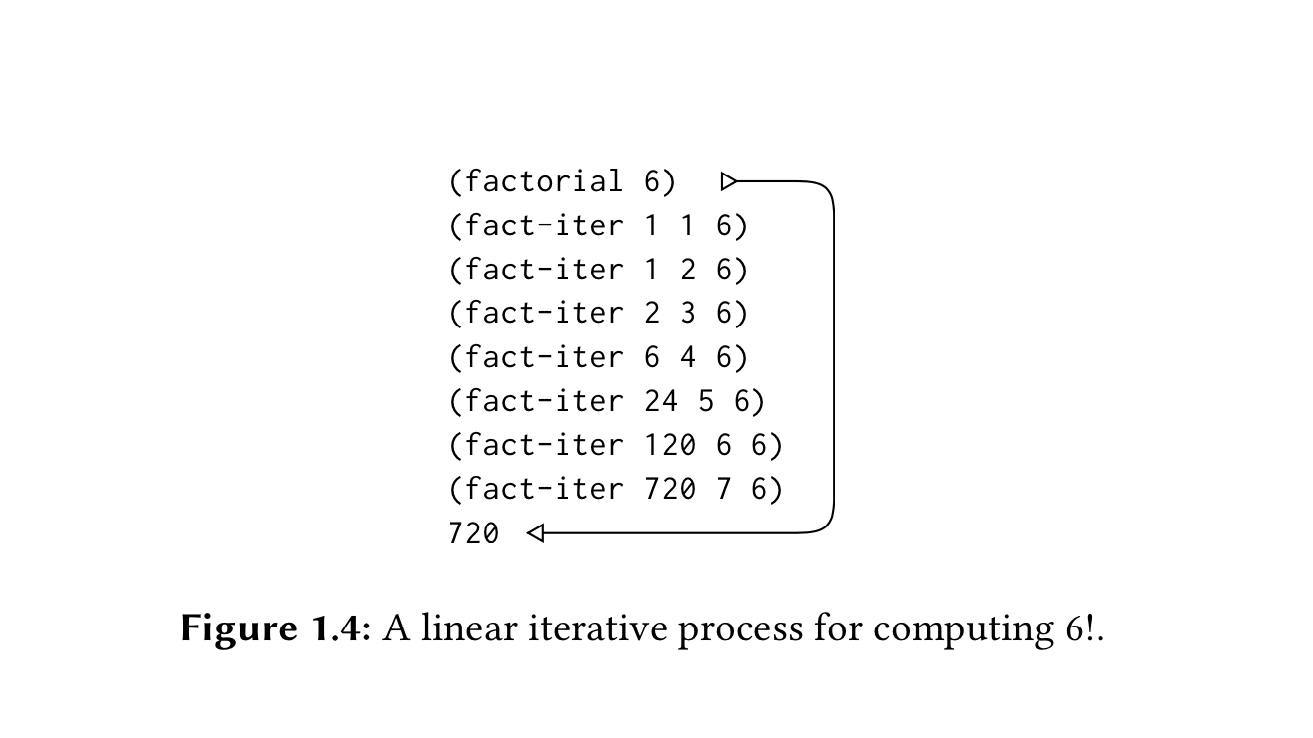
أما السابق كان توسعًا ثم انكماشًا:

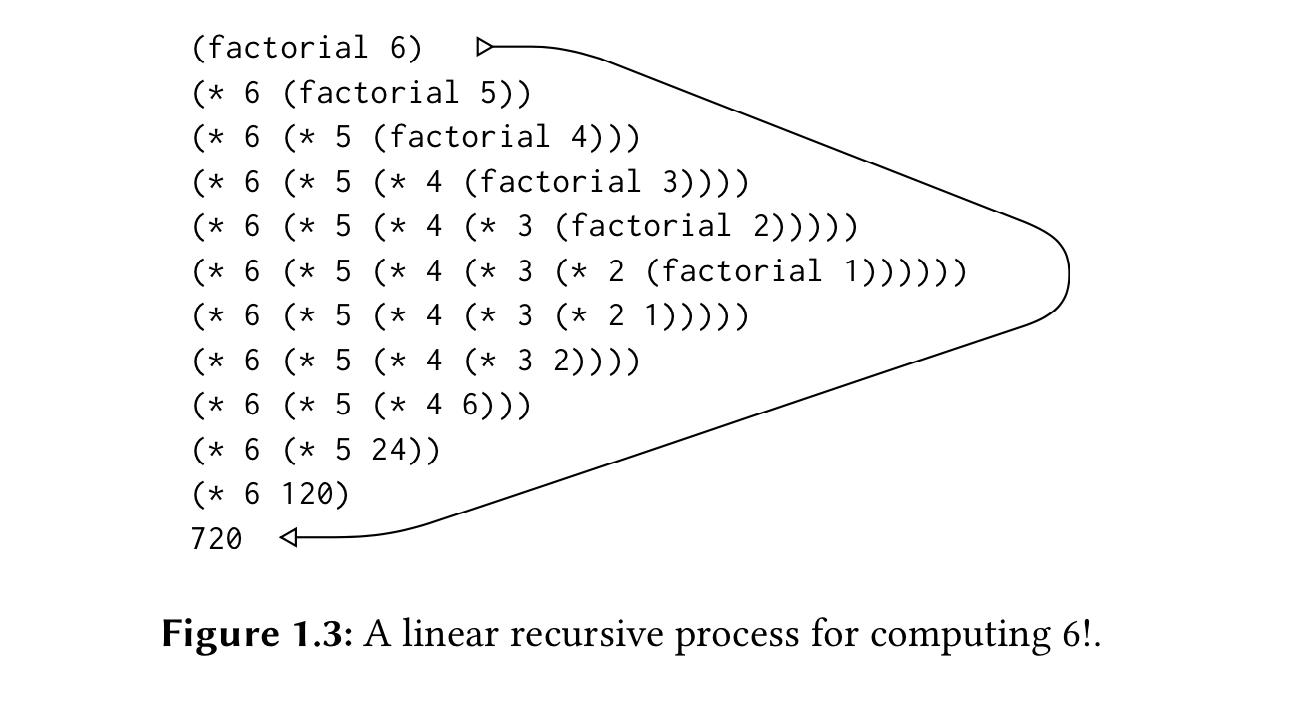
النهج الذي تتبعه كل وظيفة في سيرها مغاير للأخرى، والنتيجة نفسها!

الوظيفة الأولى تتوسع، عمليات ضرب مؤجلة، ثم تنكمش عند بدء الضرب، والمُفسِّر هاهنا يتتبع كل العمليات المؤجلة حتى ينفذها لاحقًا، فكل عملية لتعمل فإنها محتاجة إلى نتيجة العملية التالية، وهكذا فطول العمليات التي يتتبعها مساوية لحجم المدخلات، أي أنها خطية. وفي هذا النوع لو توقف البرنامج لأي سبب فلا تستطيع العودة إلى نقطة معينة، لأن كل نقطة محتاجة إلى نتيجة العملية التي تليها وإلا لن تنفذ العمليات السابقة.

أما في الوظيفة الثانية لا تتوسع ثم تنكمش، لا، كل ما يتتبعه المُفسِّر قيمتين: حاصل الضرب والعداد. قيمتان يتتبعهما المُفسِّر فقط مع قاعدة يتبعها لتغيير قيمتي المتغيرين، ولو قدر الله وتوقف البرنامج فإننا نستطيع العودة إلى نفس النقطة التي كان عليها قبل التوقف إذا وضعنا نفس القيمة التي كان عليها المتغير (حاصل الضرب) والمتغير (العداد). الكاتب سمى هذا النهج بالتكرار Iteration.

ثم قال إن أغلب اللغات المشهورة مثل C وPascal وAda تستهلك مقدارًا من الذاكرة ينمو مع عدد الاستدعاءات للوظيفة ولو كانت الوظيفة تكرارًا iteration. تفاصيل سنعرفها في الفصل الخامس، فلا تستعجل.

الخاتمة

وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وهو أول مقال من الفصل الثاني من الباب الأول!

وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.

أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.