كتاب استيعاب الخوارزميات -الفصل الثالث، الدرس الأول- العَوْدِيَّة

السلام عليكم ورحمة الله تعالى وبركاته، هذا الدرس الأول من الفصل الثالث من كتاب «استيعاب الخوارزميات Grokking Algorithms»، الكتاب الذي بدأنا بشرحه، وكان آخر درس منه «خوارزمية الفرز بالانتقاء».

مقال اليوم طويل بعض الشيء، فسأشرح مفهوم العَوْدِيَّة، والعَوْدِيَّة تقنية كثيرة الاستعمال في خوارزميات شتى.

لذا جهز نفسك، وجهز مشروبك المفضل، شاي أخضر، قهوة، ساكي!!، فإننا سنتطبق أمثلة برمجية.

سيلي مقال اليوم مقال ثانٍ بعنوان الكدسة Stack، فتأهب وافهم درس اليوم!

لكن قبل البدء سنتعرف على مفهوم هام لا مندوحة للمبرمج عنه، وهو شبه الرِمَاز Pseudocode.

شبه الرِمَاز

شبه الرِمَاز Pseudocode: وصفٌ لخوارزمية أو رِمَاز بلغة الإنسان، وهو موجهٌ له لا الآلة.

عادةً يُستعمل شبه الرِمَاز في البحوث العلمية والكتب المدرسية لشرح خوارزمية بلغة يفهمها الجميع على اختلاف لغاتهم، وأقصد باللغة هاهنا اللغة البرمجية، مثلًا فلان يعرف لغة الثعبان python والآخر لغة سي C، وهلم جرًّا…

وشبه الرِمَاز تسهيل لفهم الخوارزمية، فيَسهُل نقلها إلى اللغة البرمجية التي يجيدها المتلقي.

شبه الرِمَاز ليس خاصة بشرح خوارزمية، يفضل أن يبدأ المبرمجون بكتابة برنامجهم أو مشروعهم على الورق أو رقميًا برسمه، ليسهل عليهم بناؤه.

تود رؤية مثال بشبه الرِمَاز؟
افترض أن لدينا بُريمج لجمع رقمين، يستقبل الرقم الأول والثاني من المستخدم ويجمعهما ويعرضهما على الشاشة.

تمثيله بشبه الرِمَاز:
١. اقرأ الرقم الأول والثاني
٢. اجمعها
٣. اعرض جمعهما على الشاشة

أما كتابة بُريمج لعرض الرقم الأكبر، سيكون شبه رِمَازه:
١. أنشئ ثلاثة متغيرات، هي أ، ب، ج
٢. اقرأ الرقم أ والرقم ب من المستخدم
٣. إذا كان الرقم أ أكبر من ب فغير قيمة المتغير ج إلى قيمة المتغير أ
٤. إن لم يكن كذلك فغير قيمة المتغير ج إلى قيمة المتغير ب
٥. اعرض قيمة المتغير ج

ومن خلال شبه الرِمَاز السابق نقدر بسهولة على تحويله إلى رِمَاز بلغة python:

# Step 1: Declare variables num1, num2, and max
num1 = 0
num2 = 0
max = 0

# Step 2: Read num1 and num2 from user
num1 = int(input("Enter first number: "))
num2 = int(input("Enter second number: ")) 

# Step 3: If num1 > num2, set max to num1, otherwise set max to num2
if num1 > num2:
    max = num1
else:
    max = num2

# Step 4: Print the value of max
print("The maximum of", num1, "and", num2, "is", max)

في بعض الأحيان قد يكتب أحدهم بلغته الإنگليزية شبه رِمَاز لفعل شيء ما فيستعمل في كتابته لشبه الرِمَاز أسلوب كتابة شبيه بلغة البرمجة الفلانية، ويسمى ذلك شبه رِمَاز لغة C، أي على أسلوب لغة C، ويكون شبه رِمَاز شبيه بلغة C لكنه ليس هو، فلو نقلته لن يعمل.

أعذرني عن حشر هذه النصيحة، بعض المبرمجين إذا أرادوا كتابة برنامج شرعوا بفتح محرر النصوص وكتابة الرِمَاز دون تخطيط، وهذا النهج المُتبَع سيئ، بل فاسد تمامًا، ويظهر فساده جليًّا إذا أراد إضافة ميزة أو حذف شيء وتعديله، بالمختصر إذا زاد تعقيد المشروع.

وهذا الخطأ الشنيع سببه الاعتياد على طريقة المدرسة في حل المشكلات فكتابة الرِمَاز نشاط مختلف تمامًا عما تعلمناه في المدرسة، فقبل كتابة البرنامج عليك التخطيط وتبيين بنيته، بالمختصر المفيد عليك كتابته نظريًا قبل الشروع في كتابة الرِمَاز.

قد يقول المبتدئ: إني أكتب برامجًا ولا أخطط لها ولا أتعب نفسي بما تقول، بل أفتح محرر النصوص وأكتب البرنامج ولا أعاني!

قد يعمل ذاك المنهج العقيم في حال كتبتَ بُريمجًا صغيرًا لا برنامجًا، لكن في حال البرامج الكبيرة في الشركات والمؤسسات، وحتى في المشاريع الشخصية المتوسطة فهذا نهج فاسد، وسيتعب المبرمج بل سيعاني منه.

تُقسَّم دورة حياة البرمجية life circle of software في هندسة البرمجيات software engineering إلى خمس مراحل، وكتابة الرِمَاز المرحلة الرابعة، فهل ذلك عبثي؟

والآن حان وقت التعرف على العَوْدِيَّة!

العَوْدِيَّة

الجملة الطريفة تقول: لتعلم العَوْدِيَّة عليك فهم العَوْدِيَّة!

لم تفهمها؟
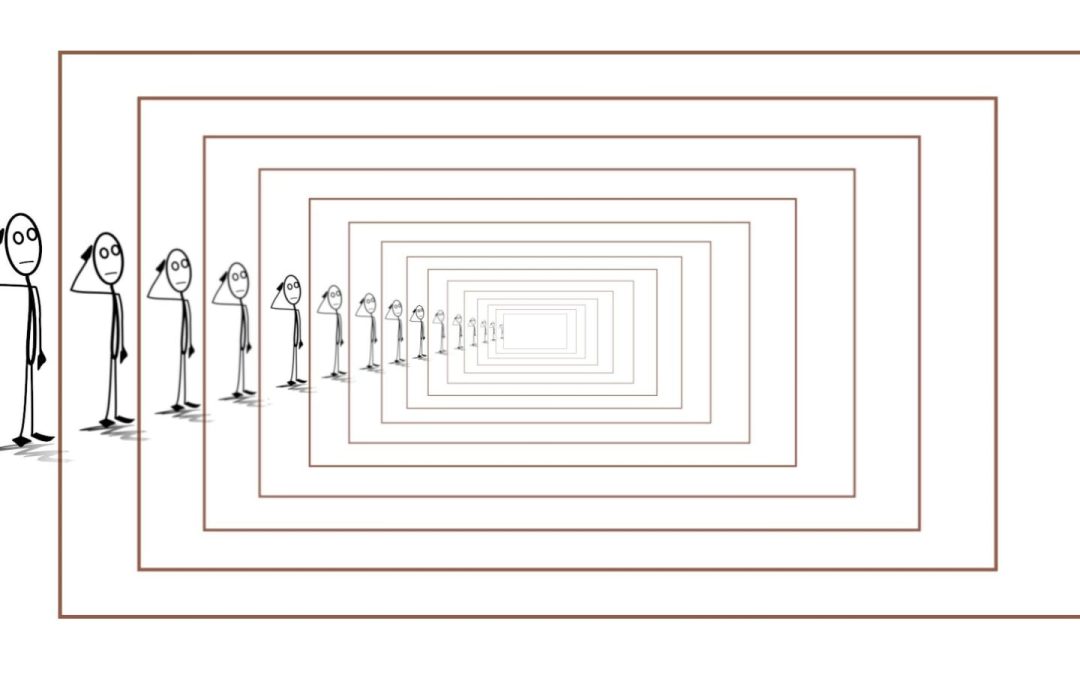
ستفهم اليوم طرافتها بعد فهمك العَوْدِيَّة، فاصبر، وحتى ذلك الحين سأخبرك عن عبود. قابلت صاحبنا عبود قبل كتابة هذا المقال، وقد قال لي: في الصباح، بحثت في القبو عن غَرَضٍ، وأثناء بحثي عثرت على حقيبة لجدتي، حقيبة غامضة!

وعثرت على صندوق كبير يضم داخله صناديق أصغر، وبعض الصناديق الصغيرة قد تحوي صناديق أصغر داخلها.

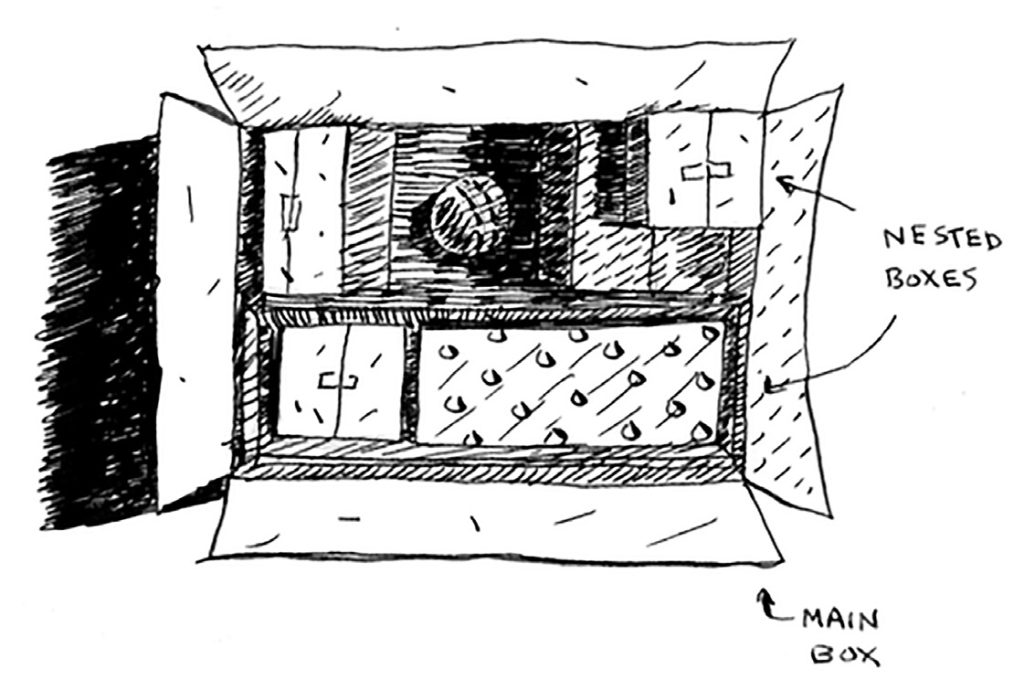
المزعج يا مبعسس أن الحقيبة مقفلة بقفل، ولا أعلم أين المفتاح، وسألت جدتي عنها فاخبرتني بأن المفتاح في أحد الصناديق، لكنها لا تتذكر أي صندوق هو.

لو كنت في مكاني يا مبعسس فأي خوارزمية ستخترع للعثور على المفتاح؟

انتهى حديث عبود، وعليك التفكير بخوارزمية لمساعدة صاحبنا عبود، فإنه ينتظر رسالةً مني. فكر بحل (خوارزمية) قبل إكمال قراءة المقال!

هذا حل -مكتوب بشبه الرِمَاز- لعلك فكرت فيه:

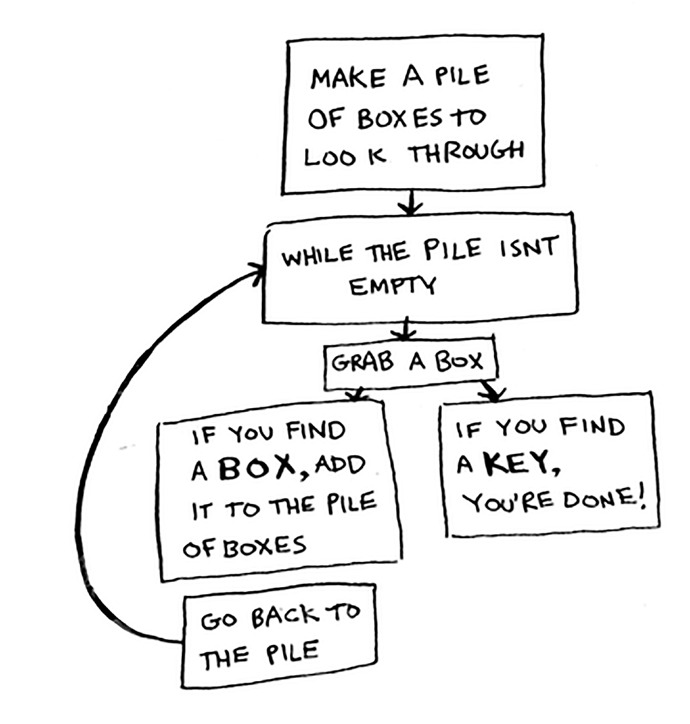
١. اجلب كومةً pile من الصناديق
٢. التقط صندوقًا وابحث داخله
٣. إذا عثرت على صندوق بداخل الصندوق الحالي فارمه لكومة الصناديق للبحث عنه لاحقًا
٤. إذا عثرت على المفتاح داخل الصندوق فتوقف
٥. كرر الخطوات السابقة حتى تعثر على المفتاح 

وهذا حل آخر بأسلوب مختصر:

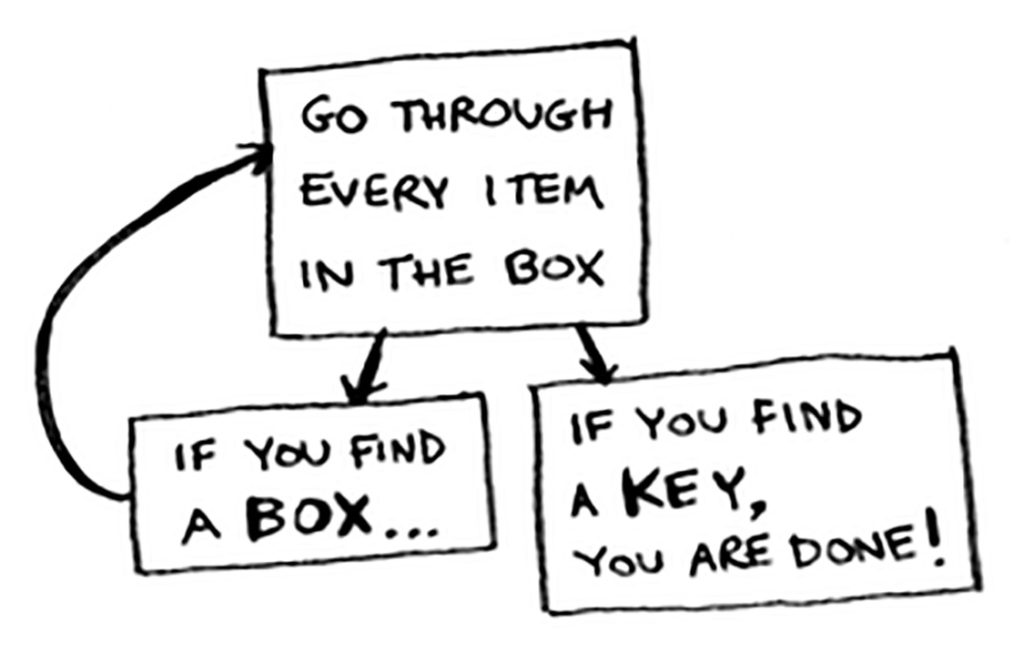
١. التقط صندوقًا وابحث داخله
٢. إذا عثرت على صندوق داخل الصندوق الحالي فعُد إلى الخطوة الأولى
٣. إذا عثرت على المفتاح فتوقف

فأي الحلين أسهل لعبود؟

سنمثل الحلين بشبه رِمَاز لغة الثعبان python، على أسلوبها. الحل الأول يستعمل حلقة التكرار while. إذا انتهت كل الصناديق من الكومة فتوقف:

سنمثل الحل الثاني باستعمال العَوْدِيَّة:

العَوْدِيَّة recursion: عملية استدعاء الوظيفة function لنفسها، استدعاء ذاتي متكرر.

وكما ترى فالحل الثاني أوضح وأسهل، على الأقل عندي، لكني سأسوق لك أمثلة كثيرة فلا تخرج من المقالة إلا وأنت مُجيد للعَوْدِيَّة تفهمها فهمًا.

قد لا يكون في استعمال العَوْدِيَّة حسن أداء لبرنامجك، وحلقات التكرار أحسن له في الأداء، وقد أورد كاتب الكتاب اقتباسًا عن ذلك أسوقه لك:

 

قد تحقق حلقات التكرار منفعة في أداء البرنامج، أما العودية فمنفعتها في أداء المبرمج. فاختر إحداهما حسب حالك واحتياجك!

 

Loops may achieve a performance gain for your program. Recursion may achieve a performance gain for your programmer. Choose which is more important in your situation!

يُخطئ في نطقها الكثير فينطقونها بضم حرف العين، كأنها مشتقة من العُود، وهذا خطأ فهي بفتح العين لا ضمها، لأنها من العَوْدَة، فالوظيفة تستدعي نفسها وتعود مرة أخرى وتستدعي نفسها، وهكذا…

لذا يسميها بعضهم التواتر أو الترداد، لكني سأعتمد على لفظة العَوْدِيَّة، اتباعًا للجامعة السورية، التي اعتمد عادة على ترجمة المصطلحات منها.

جُزأي العَوْدِيَّة

بعد أن عرفنا مفهوم العَوْدِيَّة، عليك معرفة أجزائها، لِمَ؟ ما الفائدة؟
بما أن العَوْدِيَّة استدعاء ذاتي متكرر للوظيفة من داخل رِمَازها، فإنه يسهل كتابة وظيفة تعمل بلا توقف، غير نهائية، أي متناهية!

لنفترض أنك ترغب بكتابة وظيفة تطبع الأرقام تنازليًا باستعمال العَوْدِيَّة، تعطيها الرقم ثلاثة وتطبق لك: ٣…٢…١

حاول كتابة الوظيفة قبل رؤية الحل، لنختبر فهمك لمفهوم العَوْدِيَّة.

الوظيفة باستعمال العَوْدِيَّة:

def countdown(number):
    print(number)
    countdown(number-1)

كتبنا وظيفة وسميناها countdown، وهذه الوظيفة تستقبل متغيرًا، واسم المتغير number، أي رقم. وفي جسم هذه الوظيفة طبعنا الرقم الذي تستقبله الوظيفة.

السطر الأخير، العَوْدِيَّة، استدعاء ذاتي للوظيفة، أي أن الوظيفة تستدعي نفسها بنفسها، وفي هذا الاستدعاء ينقص الرقم بمقدار واحد.

أي أننا لو شغلنا هذه الوظيفة مع الرقم ثلاثة:

countdown(3)

ستعمل الوظيفة، وفي السطر الأول فيها ستطبع الوظيفة الرقم ثلاثة، وعند سطر العَوْدِيَّة ستستدعي الوظيفة نفسها، لكن في هذا الاستدعاء سيكون الرقم اثنين.

انظر إذا عوضنا قيمة المتغير number بالقيمة المطلوبة:

countdown(3-1)

وثلاثة ناقص واحد يساوي اثنين، أي أن الدالة ستعمل مرة أخرى بقيمة مختلفة هي الاثنين، وعندما تصل إلى سطر العَوْدِيَّة ستستدعي نفسها مرة أخرى بقيمة مختلفة هي الواحد وهكذا…

وكما ترى فالدالة تعود وتعمل وتعود وتعمل، تكرار ذاتي مستمر، لهذا اسمها العَوْدِيَّة.

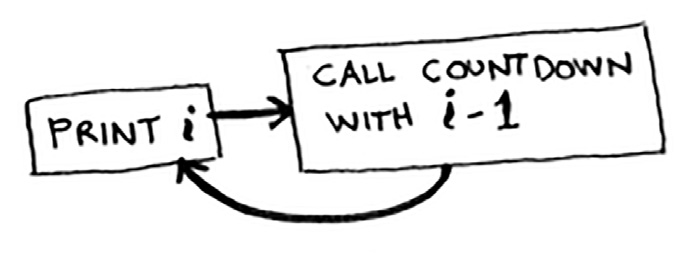
جرب تشغيل الرِمَاز السابق على حاسوبك، سترى بأن الحاسوب دخل في حلقة غير نهائية، متناهية. اضغط على زر Ctrl+C ليتوقف.

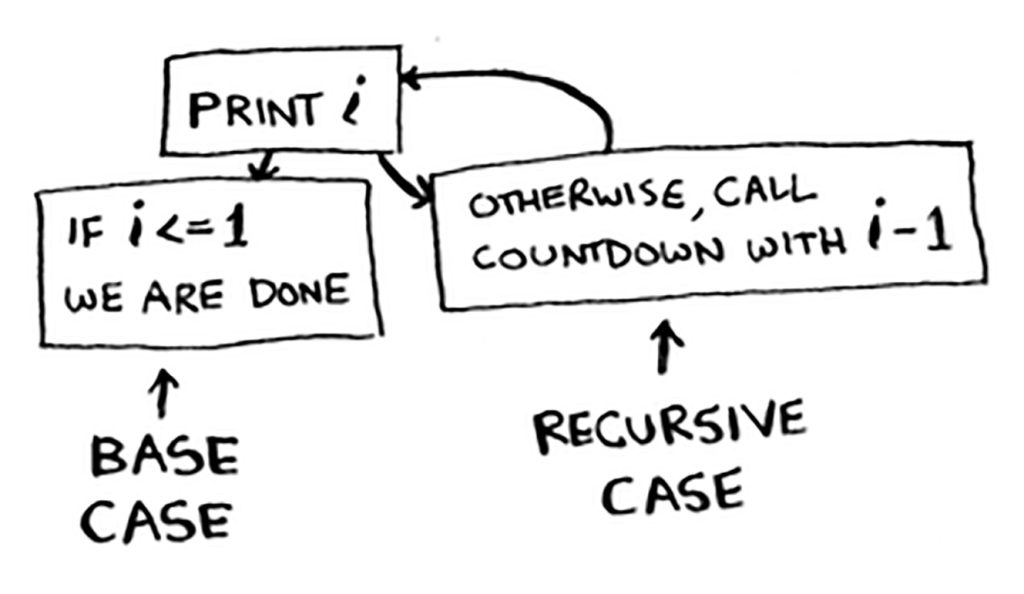
لتجنب كتابة وظيفة عَوْدِيَّة متناهية العمل عليك معرفة أجزاء العَوْدِيَّة. تتكون العَوْدِيَّة من جزئين:

١. جزء التوقف base case
٢. الجزء العَوْدِي recursive case

جميع الوظائف العَوْدِيَّة لديها الجزئين السابقين. جزء التوقف حيث تتوقف الوظيفة العَوْدِيَّة عند تحقيق شرطٍ ما، والجزء العَوْدِي حيث تستدعي الوظيفة نفسها.

في مثالنا السابق عن كتابة وظيفة تطبع الأرقام تنازليًا باستعمال العَوْدِيَّة، ليس لدينا سوى الجزء العَوْدِي، حيث تستدعي الوظيفة نفسها، وليس لدينا جزء التوقف.

لنضيف جزء التوقف إلى وظيفتنا السابقة:

def countdown(number):
    print(number)
    if number <= 0:
        return
    else:
        countdown(number-1)

جزء التوقف يوقف العَوْدِيَّة إذا كان الرقم number أصغر من الصفر أو يساويه.

سنرى مثالًا آخر لتطبيق العَوْدِيَّة، متتالية أو متسلسلة فيبوناتشي Fibonacci sequence. المهم أن تفهم المثال المعطى سابقًا فهمًا ثم أكمل المقالة.

يجدر الإشارة إلى أن جزء التوقف base case حيث تُحَلُّ المسألة مباشرةً، فما الوظيفة إلا لحل مسألة، أما الجزء العَوْدِي recursive case حيث تعمل الوظيفة على حل المسألة، ففي هذا الجزء نعمل على حل المسألة بتقسيمها إلى أجزاء، مسائل فرعية، ونحل مسألة فرعية في كل استدعاء حتى نصل إلى جزء التوقف.

متتالية فيبوناتشي

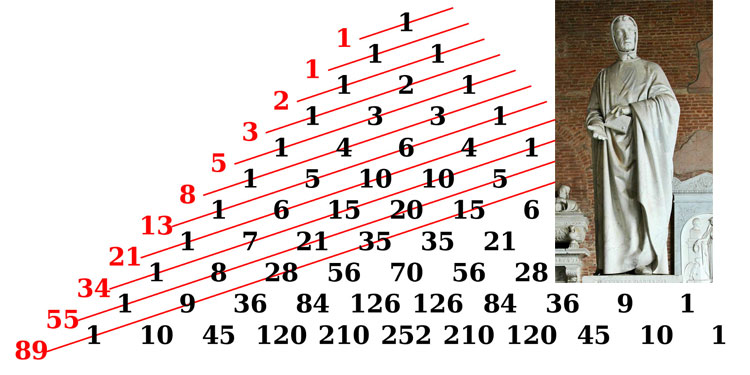
هذا أول مثال عملي لفهم العَوْدِيَّة، وهو مثال كثير الاستعمال في شرح مفهوم العَوْدِيَّة، وقد استُعملَ في كتاب الساحر SICP، لأن لغات برمجية مثل Lisp لا تحوي حلقات تكرار بل تستعيض عنها بالعَوْدِيَّة.

ما متتالية فيبوناتشي؟

متتالية فيبوناتشي: متتالية يساوي فيها الحد مجموع الحدين السابقين له.
وهي متتالية رياضية في الرياضيات، وسميت بهذا الاسم نسبةً إلى عالم الرياضيات الإيطالي ليوناردو فيبوناتشي.

تبدأ أعداد المتتالية من الرقم صفر، وثم الواحد، وثم الواحد، وثم الاثنين، وثم الثلاثة، وثم الخمسة، وثم الثمانية، وهلم جرًا:
أعداد المتتالية= ٠ ،١ ، ١، ٢، ٣، ٥، ٨، ١٣، ٢١، ٣٤…

بعض المدارس تحذف الصفر وتبدأ من الواحد، وكما ترى كل حد يساوي مجموع الحدين السابقين. الحد ٢ يساوي مجموع الحدين السابقين وهما ١ و١، والحد ١٣ يساوي مجموع الحدين السابقين وهما ٨ و٥.

بما سبق نستنتج صيغة رياضية لمتتالية فيبوناتشي:
ف(س) = ف(س-١) + ف(س-٢)
كتبنا دالة رياضية اسمها ف، اختصارًا لكلمة فيبوناتشي، وتستقبل عددًا هو س، وهذه الدالة الرياضية دالة عَوْدِيَّة، تستدعي نفسها.

بما أنك فهمت متتالية فيبوناتشي سنمثلها برمجيًا، دالة تستقبل عددًا وتستدعي نفسها مرتين، مرة ف(س-١) والمرأة الثانية ف(س-٢)، وتجمع ناتج الاستدعائين:

def fib(n):
    return fib(n-1)+fib(n-2)

هل هذا الرِمَاز كافيًا أم نسيت شيئًا؟
بل نسيت، ستعمل هذه الوظيفة للأبد، وظيفة متناهية، فقد نسينا إضافة جزء التوقف base case، لكن ما جزء التوقف لهذه الوظيفة؟

وتسألني هذا السؤال؟!
افهم متتالية فيبوناتشي فهمًا. جزء التوقف سيكون إذا وصلت الوظيفة إلى الرقم صفر أو واحد. إذن ستكون الوظيفة:

def fib(n):
    if n in [0,1]: return n
    return fib(n-1)+fib(n-2)

print(fib(8))

جربها عندك برقم ٨ لنرى النتيجة، كما سطر الطباعة print، وسيظهر لك العدد ٢١، لأنه الرقم الثامن في المتتالية في حال بدأنا المتتالية من الرقم واحد.

جرب إضافة حلقة تكرار تبدأ من الصفر حتى الرقم ٨ لترى المتتالية:

def fib(n):
    if n in [0,1]: return n
    return fib(n-1)+fib(n-2)
for i in range(9):
    print(fib(i))

وهذه متتالية فيبوناتشي بلغة سي C:

#include <stdio.h>

// fibonacci() funtion definition
int fibonacci(int num)
{
    // first base condition check
    if (num == 0)
    {
        return 0; // retuning 0, if condition meets
    }
    // second base condition check
    else if (num == 1)
    {
        return 1; // returning 1, if condition meets
    }
    // else calling the fibonacci() function recursively till we get to the base conditions
    else
    {
        return fibonacci(num - 1) + fibonacci(num - 2); // recursively calling the fibonacc() function and then adding them
    }
}

int main()
{
    int num; // variable to store how many elements to be displayed in the series
    printf("Enter the number of elements to be in the series : ");
    scanf("%d", &num); // taking user input
    int i;
    for (i = 0; i < num; i++)
    {
        printf("%d, ", fibonacci(i)); // calling fibonacci() function for each iteration and printing the returned value
    }

    return 0;
}

ترغب أن ترى ماذا يحدث إذا شغلنا الرِمَاز بقيمة هي ٥؟

سترى شجرة عَوْدِيَّة:

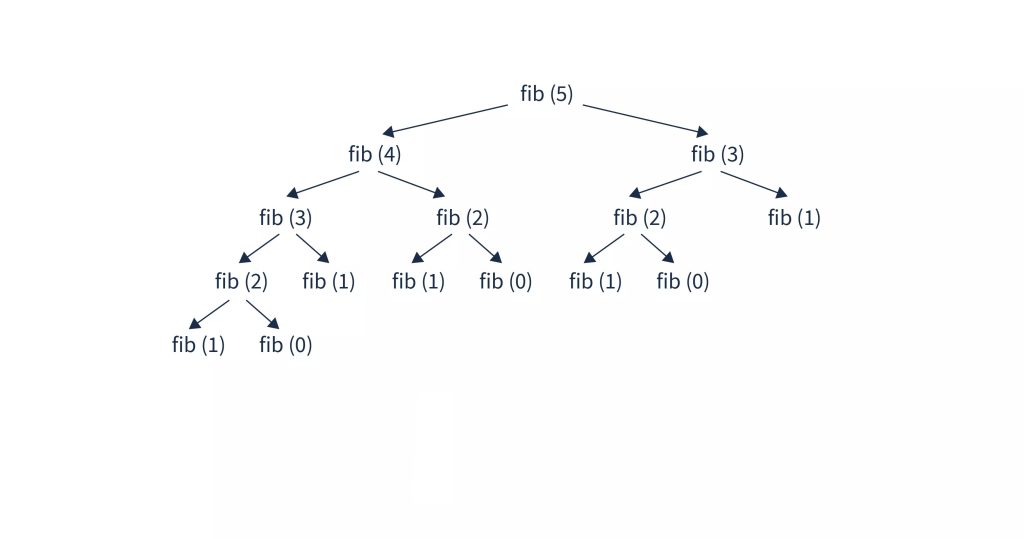
وكما ترى في كل استدعاء للوظيفة تنقسم الوظيفة إلى جزئين، إذا شغلنا الوظيفة بالرقم ٥، فإن الوظيفة تنقسم إلى وظيفتين فرعيتين، هما ف(٤) وأيضًا ف(٣)، وكل وظيفة فرعية تنقسم إلى وظيفتين فرعيتين، وهكذا حتى نصل إلى شرط التوقف إن كان يساوي الصفر أو الواحد.

تتذكر درس رمز O الكبير؟
ما رمز O الكبير لرِمَازنا السابق؟

سيكون (س²)O، لأن الوظيفة تنقسم إلى وظيفتين فرعيتين.

العاملي بالعَوْدِيَّة

هل تتذكر العاملي الذي شرحناه في درس تعقيد الوقت ورمز O الكبير؟
ما رأيك بتطبيقه اليوم برمجيًا باستعمال العَوْدِيَّة؟
كثرة الأمثلة تقوي الفهم وتثبته، فطبق الأمثلة ولا تنس!

قلنا إن العاملي الخمسة يساوي ضرب كل الأعداد المساوية أو الأصغر من الرقم خمسة ما عدا الصفر، إذن لتمثيله رياضيًا سنكتب دالة رياضية عَوْدِيَّة:
ع(س) = س * ع(س-١)
وشرط التوقف أن يكون س يساوي الصفر. حاول كتابته قبل رؤية الحل.
تمثيل الدالة الرياضية السابقة بوظيفة برمجية سيكون:

def factorial(n):
    if n == 0: return 1
    return n*factorial(n-1)

جربها عندك بتشغيلها.
سنتتبع خطوات تشغيلها، افترض أنك شغلتها مع عاملي الثلاثة:

factorial(3)

ستبدأ الوظيفة العمل، وستتنفذ عبارة التحقق if، جزء التوقف base case، وترى أن الرقم لا يساوي الصفر، لذا تستمر بالعمل للسطر الثاني، الجزء العَوْدِي:

return n*factorial(n-1)

في هذا السطر يعوض المتغير س n بالرقم ٣، فيصبح السطر بعد التعويض:

return 3*factorial(3-1)

أما بعد العملية الرياضية، ٣-١، سيكون السطر:

return 3*factorial(2)

الآن تبدأ العَوْدِيَّة، تستدعي الوظيفة نفسها بالرقم ٢، كما ترى في الأعلى، وهذه هي أول مرة استدعاء، فتذكرها.

وتبدأ الوظيفة العمل من البداية، وتتحقق من العدد هل يساوي الصفر أم لا فإن لم يساوه، ذهبت إلى الجزء العَوْدي، وسيكون هذا الجزء بعد عملية التعويض:

return 2*factorial(1)

وهنا تبدأ عملية الاستدعاء الثانية، ستبدأ الوظيفة بالعمل مرة ثالثة، وهذه المرة بالرقم واحد، وستدخل إلى الجزء العَوْدي، وسيكون بعد التعويض:

return 1*factorial(0)

وهذه هي مرة الاستدعاء الثالثة، وكما ترى فإن الرقم أصبح صفرًا. وستستدعي الوظيفة نفسها لآخر مرة، وتكون عملية الاستدعاء الرابعة والأخيرة، لأن الشرط تحقق، أصبح الرقم صِفرا.

إذن فإن النتيجة التي سترجعها الوظيفة في الاستدعاء الرابع هي الرقم واحد، الموضوع في شرط التوقف، وسنمرره لعملية الاستدعاء الثالث، لذا فإن نتيجة الاستدعاء الثالث:

return 1*1

يساوي واحد، فواحد ضرب واحد واحد، ونتيجة الثالث سنمرره للاستعداء الثاني:

return 2*1

والنتيجة اثنين، وسنمرر نتيجة الاستدعاء الثاني لأول استدعاء:

return 3*2

إذن فالنتيجة النهائية هي ستة ٦، لأن اثنين ضرب ثلاثة يساوي الستة.

أرأيت كيف تعمل العَوْدِيَّة؟
أرجو بأنك فهمت، مر على الخطوات السابقة وكررها إن لم تفهم.

وهذا رِمَاز بلغة سي C للوظيفة السابقة:

#include <stdio.h>

int factorial(int n) {
    if (n == 0) {
        return 1;
    }
    else {
        return n * factorial(n - 1);
    }
}

int main() {
    printf("%d\n", factorial(3));
    return 0;
}

الأس بالعَوْدِيَّة

وهذا المثال الأخير في مقالنا، سنكتب وظيفتنا التي ترجع نتيجة رفع عدد ما لأس معين.
وكما سبق وشرحنا الأسس في الدرس الأول من الكتاب، تجده هنا، فإن الأس ليس إلا عدد المرات التي يُضرب فيها الأساس في نفسه.

مثلا الرقم ٥²، ليس إلا الرقم خمسة مضروب في نفسه مرتين.

سنكتب وظيفتنا الآن بلغة الثعبان python:

def power(base, exponent):
    if exponent == 0: return 1
    return base*power(base, exponent-1)

شغله مع وضع الأساس ٢ والأس ٣، وسترجع لك الوظيفة الرقم ٨.

التمرين: عليك توضيح خطوات سير الوظيفة السابقة كما فعلنا مع وظيفة العاملي.
وتمرين آخر سهل يسير، اكتب وظيفة باستعمال العَوْدِيَّة لحساب الأعداد من الرقم واحد حتى س.

الخاتمة

أتتذكر الجملة الطريفة في بداية مفهوم العَوْدِيَّة؟
لتعلم العَوْدِيَّة عليك فهم العَوْدِيَّة!
كأننا دخلنا في عَوْدِيَّة متناهية، جميلة طريفة 🙂

وها أنا أخط بقلمي الخطوط الأخيرة لهذا المقال الشائق، وأرجو إني قد وفِّقت في شرح العَوْدِيَّة وتقريبها من الأذهان.

وفي نهاية الأمر لا يسعني سوى أن أشكرك على حسن قراءتك لهذا المقال، وأني لبشر أصيب وأخطِئ، فإن وفِّقت في طرح الموضوع فمن اللّٰه عز وجل وإن أخفقت فمن نفسي والشيطان.

أرجو منك تقييم كفاءة المعلومات من أجل تزويدي بالملاحظات والنقد البناء في خانة التعليقات أو عبر حساب الموقع، والسلام عليكم ورحمة اللّٰه تعالى وبركاته.